Fonctionnement de l’évaluation de la sensibilité à l’incertitude attributaire

L’outil Évaluer la sensibilité à l’incertitude attributaire évalue la manière dont les résultats d’analyse de certains outils de la boîte à outils Statistiques spatiales changent lorsque les valeurs d’une ou de plusieurs variables d’analyse (attributs) sont incertaines. L’incertitude attributaire peut être spécifiée à l’aide de marges d’erreur, de limites supérieure et inférieure ou d’un pourcentage spécifié de la valeur d’origine. Cet outil accepte les entités en sortie des outils suivants :

• Analyse de point chaud (Getis-Ord Gi*)
• Analyse de points chauds optimisée
• Analyse de grappes et de valeurs aberrantes (Anselin Local Morans I)
• Analyse de points aberrants optimisée
• Régression linéaire généralisée
• Autocorrélation spatiale (Global Moran's I)

L’outil effectue une analyse de la sensibilité en simulant à plusieurs reprises de nouvelles données à l’aide de la variable d’analyse d’origine et de sa mesure d’incertitude. Il réexécute ensuite l’outil d’analyse d’origine plusieurs fois avec les données simulées et synthétise les résultats. Si les résultats des simulations sont proches des résultats d’origine, vous saurez que les résultats d’origine sont robustes et fiables. Toutefois, si les simulations produisent des différences importantes par rapport aux résultats d’origine, ne tirez pas de conclusions hâtives des résultats d’origine.

Applications possibles

Voici quelques applications possibles de l’outil :

• Une organisation caritative locale utilise l’analyse des points chauds afin de hiérarchiser les zones du comté dans lesquelles intervenir pour réduire la pauvreté. Elle prévoit de se focaliser sur les régions où l’analyse indique une concentration et une intensité de la pauvreté élevées (points chauds avec un niveau de confiance de 99 pour cent). En surveillant l’évolution des points chauds, l’organisation peut décider de renforcer sa présence ou revoir ses priorités.
• Une chaîne de vente au détail de grande envergure a développé un modèle de régression linéaire généralisée pour estimer l’influence des facteurs démographiques (âge et revenu disponible, par exemple) sur les ventes d’articles de sport. Les variables explicatives collectées via les enquêtes menées incluent à la fois des limites supérieure et inférieure. En intégrant l’incertitude dans ces variables, le détaillant peut étudier la plage potentielle du volume des ventes.

Incertitude attributaire

L’incertitude attributaire désigne la variabilité des valeurs de données résultant des caractères naturels et inévitables de la collecte et de l’agrégation de données, comme une erreur d’échantillonnage ou une erreur de mesure. Des erreurs d’échantillonnage se produisent lorsque les données sont collectées à partir d’un sous-ensemble d’une population, ce qui soulève des questions relatives à la représentativité de l’échantillon pour l’ensemble de la population. Une erreur de mesure survient lorsqu’un instrument de collecte de données, par exemple un thermomètre ou un anémomètre, insuffle des variations mineures dans les valeurs enregistrées par rapport aux valeurs véritables. Les données sont souvent fournies avec la meilleure estimation de la véritable valeur de la mesure, appelée estimation ponctuelle, et la mesure de son niveau d’incertitude. Bien que ces sources d’incertitude puissent affecter la précision des données, elles sont présentes dans tout processus de collecte de données du monde réel. Reconnaître et explorer l’incertitude attributaire et son impact sur les résultats d’analyse permet de rendre les analyses plus transparentes et performantes.

Mode de quantification de l’incertitude

Cet outil prend en charge trois façons de spécifier l’incertitude attributaire : la marge d’erreur, les limites supérieure et inférieure et un pourcentage au-dessus et en dessous d’une valeur attributaire.

Marge d’erreur

Une marge d’erreur représente la plage dans laquelle la véritable valeur de l’attribut se trouvera probablement. Elle est associée à un niveau de confiance (par exemple 90 pour cent), qui indique dans quelle mesure vous pouvez être certain que la valeur réelle de l’attribut est comprise dans la plage définie par l’estimation, plus ou moins la marge d’erreur. Par exemple, une enquête peut estimer qu’un comté compte 2 500 personnes souffrant de pauvreté, avec une marge d’erreur de 300 au niveau de confiance de 90 pour cent. Cela signifie que vous pouvez être sûr à 90 pour cent que le véritable nombre de personnes souffrant de pauvreté se situe entre 2 200 et 2 800. Avec cette méthode, un champ de marge d’erreur est requis pour au moins une variable d’analyse. Ce champ contient la limite d’erreur numérique qui représente où au-dessus ou en dessous de l’estimation d’échantillon la véritable valeur de la population doit se situer. Le niveau de confiance est de 90 pour cent par défaut et peut être ajusté à l’aide du paramètre Niveau de confiance de la marge d’erreur.

Remarque :

Les marges d’erreur sont généralement enregistrées sous forme de champs avec la variable d’origine. C’est le cas de nombreuses variables dans les données ArcGIS Living Atlas of the World provenant de l’enquête sur la population américaine du Bureau du recensement américain (ACS). De nombreux organismes statistiques nationaux fournissent des mesures d’incertitude semblables.

Limites inférieure et supérieure

Les limites inférieure et supérieure représentent l’incertitude d’un attribut en spécifiant de manière explicite une plage autour d’une estimation. Contrairement à la marge d’erreur, les limites inférieure et supérieure n’ont pas besoin d’être symétriques autour de l’estimation ponctuelle.

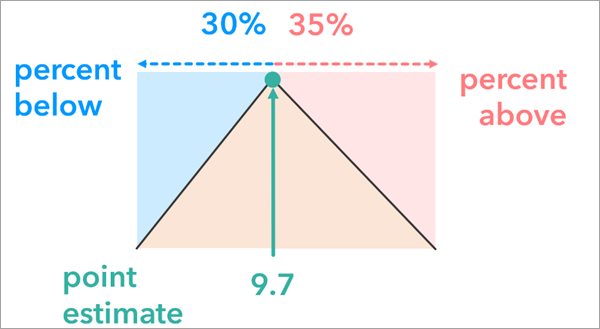
Pourcentages inférieur et supérieur

L’option Pourcentages inférieur et supérieur représente l’incertitude attributaire en ajustant la valeur attributaire d’origine de chaque entité selon un pourcentage spécifié. Elle génère une plage autour de l’estimation qui peut contenir la véritable valeur. Cette approche peut être utile lorsque d’autres méthodes, telles que la marge d’erreur ou les limites supérieure et inférieure, ne sont pas disponibles pour exprimer l’incertitude.

Remarque :

Contrairement aux options de marge d’erreur et de limites supérieure et inférieure qui permettent de spécifier l’incertitude attributaire différemment pour chaque entité, l’option de pourcentages inférieur et supérieur applique la même définition d’incertitude à toutes les entités.

Résoudre l’incertitude à l’aide de simulations

Pour évaluer la sensibilité à l’incertitude des résultats d’analyse, l’outil génère des jeux de données simulés en fonction de la variable d’analyse d’origine et de sa mesure d’incertitude. Dans l’idéal, chaque jeu de données simulé représente une version plausible des données susceptibles d’exister dans le monde réel. En outre, il existe différentes hypothèses concernant la façon dont la véritable valeur peut être centrée autour de l’estimation ponctuelle ou dispersée à partir de l’estimation ponctuelle. L’outil utilise des distributions de probabilités pour empêcher les valeurs de données simulées de capturer la plage et pour limiter la possibilité de différentes réalisations des données. Trois distributions sont prises en charge : normale, triangulaire et uniforme. Lors de la simulation de données pour la régression linéaire généralisée, la structure de corrélation entre les variables explicatives est conservée. Pour les résultats d’analyse générés par d’autres outils, les données sont simulées indépendamment de chaque entité. Pour prendre en compte la dépendance entre les variables explicatives, leur corrélation est estimée globalement et les valeurs simulées pour chaque entité sont générées en ajoutant le bruit aléatoire d’une distribution normale multivariée avec une moyenne nulle et la matrice de covariance en fonction de la corrélation globale entre les variables explicatives. Étant donné que le bruit aléatoire est basé sur une distribution normale multivariée, les simulations pour la régression linéaire généralisée ne prennent en charge que la méthode de simulation normale.

Normal

L’option Normal du paramètre Méthode de simulation est couramment utilisée lorsqu’une marge d’erreur associée à un niveau de confiance est disponible. Cette option utilise une distribution normale (ou gaussienne) des probabilités avec une moyenne égale à la valeur de la variable d’analyse d’origine et un écart type basé sur la valeur de marge d’erreur et le niveau de confiance de l’entité.

Comme le suggère la forme de la distribution des probabilités, les valeurs plus proches de l’estimation d’origine sont plus susceptibles d’être générées que celles qui sont plus éloignées. Toutefois, cela peut nettement varier selon la marge d’erreur. Les localisations avec des marges d’erreur plus importantes (souvent dues à des tailles d’échantillon inférieures) auront des distributions avec des extrémités plus longues, ce qui signifie que les simulations sont plus susceptibles de générer des valeurs plus éloignées de l’estimation d’origine.

Triangulaire

Une distribution triangulaire est généralement utilisée lorsque la valeur d’origine représente une estimation probable de la véritable valeur. L’option Triangulaire du paramètre Méthode de simulation est particulièrement utile avec les distributions asymétriques où les valeurs sont plus susceptibles de s’agréger autour de la valeur estimée, mais avec une dispersion asymétrique. Une distribution triangulaire est construite et utilisée pour simuler les données de chaque entité en fonction de la valeur minimale de données, de la valeur d’origine de l’entité et de la valeur maximale de données. La valeur du paramètre Type d’incertitude détermine les valeurs minimale et maximale de données de la distribution triangulaire.

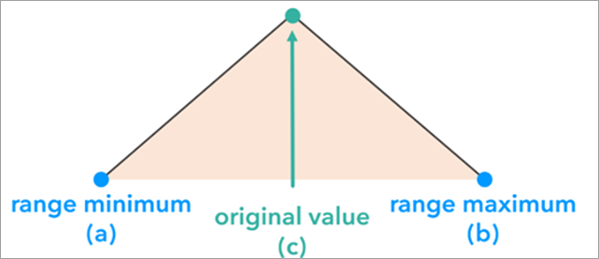
La forme de la distribution triangulaire des probabilités garantit que les valeurs proches de la valeur d’origine sont plus susceptibles d’être générées que les valeurs situées aux extrêmes de la distribution.

Remarque :

Contrairement à la distribution normale, la forme n’a pas besoin d’être symétrique. Par exemple, les limites inférieure et supérieure peuvent être différentes.

Uniforme

L’option Uniforme du paramètre Méthode de simulation est utilisée lorsque la valeur d’origine à chaque localisation est une piètre estimation de la véritable valeur et que la seule information disponible sur l’incertitude attributaire est la plage de valeurs possibles. Cette option utilise une distribution uniforme des probabilités avec deux paramètres : la valeur minimale de la plage définie par le type d’incertitude et la valeur maximale de la plage définie par le type d’incertitude. Contrairement aux distributions normale et triangulaire, la distribution uniforme n’utilise pas la valeur d’origine dans les paramètres de distribution des probabilités. Chaque valeur comprise entre le minimum et le maximum a la même probabilité d’être générée dans les simulations.

Outils pris en charge

Contrairement à la plupart des outils de géotraitement qui acceptent une couche existante en entrée, l’entrée de cet outil est la couche de résultat de l’un des outils suivants de la boîte à outils Statistiques spatiales :

• Analyse de point chaud (Getis-Ord Gi*)
• Analyse de points chauds optimisée
• Analyse de grappes et de valeurs aberrantes (Anselin Local Morans I)
• Analyse de points aberrants optimisée
• Régression linéaire généralisée
• Autocorrélation spatiale (Global Moran's I)

Outils Analyse des points chauds, Analyse optimisée des points chauds, Analyse des valeurs aberrantes et des agrégats et Analyse optimisée des points aberrants

Pour les résultats des outils Analyse des points chauds (Getis-Ord Gi*), Analyse optimisée des points chauds, Analyse des valeurs aberrantes et des agrégats (indice local de Moran d’Anselin) et Analyse optimisée des points aberrants, la stabilité est évaluée en déterminant la fréquence à laquelle une entité a changé de catégorie dans les exécutions d’analyse répétées. Par exemple, si une entité était un point chaud avec un niveau de confiance de 90 pour cent dans l’analyse d’origine et qu’elle est passée dans une autre catégorie dans l’une des exécutions à l’aide des données simulées, cela compte comme un changement de catégorie. L’outil comptabilise le nombre de fois que la catégorie d’une entité change. Les entités sont marquées comme instables si moins de 80 pour cent des simulations ont eu pour résultat la catégorie d’origine.

L’outil produit un groupe de couches contenant une couche d’instabilité et une copie des résultats d’analyse d’origine.

En outre, le groupe de couches contient un diagramme affichant le nombre d’entités pour chaque catégorie d’analyse d’origine et chaque catégorie prédominante. La catégorie prédominante est celle qui survient le plus souvent au cours de toutes les exécutions répétées de l’outil à chaque localisation.

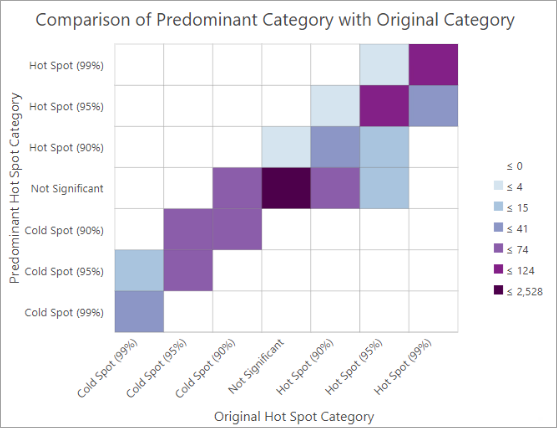
Ce diagramme peut faciliter l’identification des modèles d’instabilité catégorielle. Un résultat parfaitement stable dans lequel chaque catégorie d’origine concorde parfaitement avec la catégorie prédominante remplirait les diagonales de cellules.

Remarque :

L’outil ne prend pas en charge les résultats d’analyse des points agrégés lors de l’exécution de l’outil Analyse optimisée des points chauds ou Analyse optimisée des points aberrants.

Outil Régression linéaire généralisée

Lors de l’évaluation de l’incertitude d’une analyse de type Régression linéaire généralisée, les principaux résultats de l’outil Régression linéaire généralisée sont des diagrammes qui affichent la distribution des diagnostics de régression dans les exécutions simulées, comme les coefficients des variables explicatives et R-carré. L’outil fournit un groupe de couches contenant une copie du résultat de l’analyse d’origine, une table synthétisant les résultats des exécutions répétées de l’outil d’origine et trois diagrammes affichant la distribution des coefficients R-carré, de signification statistique de Jarque-Bera et des variables explicatives standardisées.

Outil Autocorrélation spatiale (indice global de Moran)

Pour les résultats de l’outil Autocorrélation spatiale (indice global de Moran), l’objectif de l’outil est de vous aider à identifier le degré de certitude de l’évaluation d’origine de l’autocorrélation spatiale globale avec une incertitude attributaire. L’outil fournit un groupe de couches avec une copie des résultats de l’analyse d’origine, une table synthétisant les résultats des exécutions répétées de l’outil et des diagrammes affichant la distribution des valeurs de l’indice de Moran et leurs scores z.

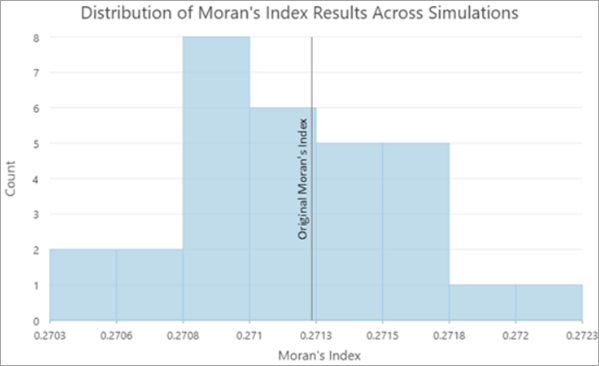
En général, la plupart des valeurs de l’indice de Moran et leurs scores z sont plus faibles que les valeurs d’origine car l’ajout de bruit non corrélé aléatoire aux valeurs de données tend à réduire l’autocorrélation spatiale des données.

Remarque :

L’outil Autocorrélation spatiale (indice global de Moran) ne génère pas d’entités en sortie. Utilisez les entités en entrée d’origine qui ont été utilisées dans l’analyse de l’outil Autocorrelation spatiale (indice global de Moran) comme valeur du paramètre Entités de résultat d’analyse.

Autres éléments à prendre en compte

Les sous-sections ci-dessous contiennent des informations supplémentaires.

Modifier le seuil de stabilité dans la sortie

Pour les résultats des outils Analyse des points chauds (Getis-Ord Gi*), Analyse optimisée des points chauds, Analyse des valeurs aberrantes et des agrégats (indice local de Moran d’Anselin) et Analyse optimisée des points aberrants, la couche d’instabilité applique un seuil de stabilité par défaut de 80 pour cent. En d’autres termes, pour qu’une entité soit considérée comme stable, elle doit avoir pour résultat la même catégorie que l’analyse d’origine dans plus de 80 pour cent des simulations. Si vous augmentez ce seuil, le nombre d’entités considérées comme instables sera plus élevé. Si vous le diminuez, le nombre d’entités considérées comme instables sera plus faible.

Le seuil qui définit la stabilité peut être configuré à l’aide des paramètres de symbologie de la couche. Pour modifier le seuil, vous devez d’abord rechercher et sélectionner la couche d’instabilité dans le groupe de couches en sortie. Ensuite, ouvrez la fenêtre Symbologie, puis double-cliquez sur la cellule de valeur Supérieure pour la classe 80 pour cent et modifiez la valeur de seuil.

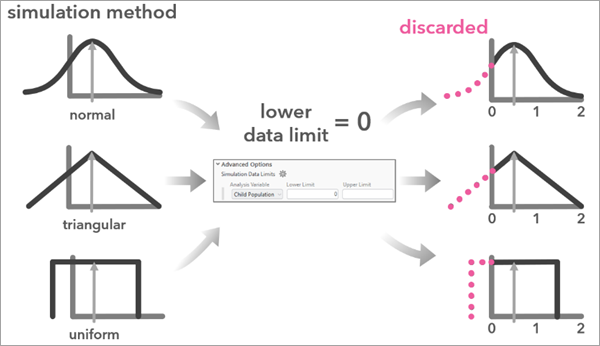
Limites des données de simulation

Vous pouvez définir des limites sur la plage des valeurs simulées pour une variable d’analyse. Cela peut être utile lorsque la variable d’analyse ne doit pas être négative (nombres) ou lorsque sa plage doit être comprise entre zéro et 100 (pourcentage). Utilisez le paramètre Limites des données de simulation pour définir la plage des valeurs possibles pour chaque variable. Lorsque vous spécifiez une valeur pour le paramètre Limites des données de simulation, l’outil ignore les valeurs simulées qui sont générées en dehors de la plage spécifiée et répète la simulation.

Enregistrer les résultats de simulation intermédiaires

Les simulations que l’outil crée peuvent être enregistrées en tant que classes d’entités. Utilisez le paramètre Espace de travail des résultats de la simulation pour configurer un espace de travail existant dans lequel l’outil enregistre chaque résultat de simulation.

La convention d'affectation de noms de chaque fichier suit le format ci-après : Nom des entités de résultat d’analyse _ ID de la simulation _ Horodatage de la simulation. Chaque classe d’entités de résultat de la simulation contient la structure du résultat d’analyse d’origine.

Les résultats de simulation intermédiaires peuvent être utiles pour des analyses ultérieures. Par exemple, vous pouvez examiner un espace de travail des résultats de simulation de l’outil Régression linéaire généralisée pour mieux comprendre la distribution des valeurs prévues entre les simulations.

Métadonnées des opérations de géotraitement

Pour identifier l’outil d’analyse, les entités en entrée et les paramètres supplémentaires utilisés dans l’analyse, l’outil lit les métadonnées à partir de la valeur du paramètre Entités de résultat d’analyse. Par conséquent, l’analyse qui a produit les entités de résultat d’analyse doit être configurée en vue de la consignation dans les métadonnées.

Ce paramètre est activé par défaut. Pour vérifier ce paramètre, ouvrez la boîte de dialogue Options, cliquez sur l’onglet Géotraitement, puis dans la section Journalisation, vérifiez que l’option Consigner les opérations de géotraitement dans les métadonnées du jeu de données est sélectionnée.

Remarque :

L’outil ne prend pas en charge les analyses de l’outil Autocorrélation spatiale (indice global de Moran) exécutées sur des couches hébergées car les métadonnées ne peuvent pas être modifiées pour ces jeux de données.

Ressources supplémentaires

Pour plus d'informations, consultez les ressources suivantes :

• JingXiong Zhang and Michael Goodchild. 2002. "Uncertainty in Geographical Information." Taylor & Francis. ISBN 0-203-47132-6. https://doi.org/10.1201/b12624.
• Raphaella Diniz, Pedro O.S. Vaz-de-Melo, Renato Assunção. 2024. “Data augmentation for spatial disease mapping.” Spatial Data Science Symposium 2021 Short Paper Proceedings. https://doi.org/10.25436/E2KS35
• Michele Crosetto and Stefano Tarantola. 2001. "Uncertainty and sensitivity analysis: tools for GIS-based model implementation." International Journal of Geographical Information Science. 15:5, 415-437. https://doi.org/10.1080/13658810110053125
• Zhou Dimin. 2010. “Research on Propagation of Attribute Uncertainty in GIS.” 2010 International Conference on Intelligent Computation Technology and Automation.
• Hyeongmo Koo, Takuya Iwanaga, Barry F.W. Croke, Anthony J. Jakeman, Jing Yang, Hsiao-Hsuan Wang, Xifu Sun, Guonian Lü, Xin Li, Tianxiang Yue, Wenping Yuan, Xintao Liu, and Min Chen. 2020. “Position paper: Sensitivity analysis of spatially distributed environmental models- a pragmatic framework for the exploration of uncertainty sources.” Environmental Modelling and Software. https://doi.org/10.1016/j.envsoft.2020.104857
• Hyeongmo Koo , Yongwan Chun, and Daniel A. Griffith. 2018. “Geovisualizing attribute uncertainty of interval and ratio variables: A framework and an implementation for vector data.” Journal of Visual Languages and Computing 44 89-96. https://doi.org/10.1016/j.jvlc.2017.11.007
• Robert Haining, Daniel A. Grifith, and Robert Bennett. 1983. “Simulating Two-dimensional Autocorrelated Surfaces.” Geographical Analysis. https://doi.org/10.1111/j.1538-4632.1983.tb00785.x
• Sirius Fuller and Charles Gamble. 2020. "Calculating Margins of Error the ACS Way." American Community Survey (ACS) Programs and Surveys, U.S. Census Bureau.
• Shuliang Wang, Wenzhong Shi, Hanning Yuan, and Guoqing Chen. 2005. "Attribute Uncertainty in GIS Data". Fuzzy Systems and Knowledge Discovery Conference. 3614, 614-623. https://doi.org/10.1007/11540007_76
• Ningchuan Xiao, Catherine A. Calder, and Marc P. Armstrong. 2007. "Assessing the effect of attribute uncertainty on the robustness of choropleth mapclassification." International Journal of Geographical Information Science. 21:2, 121-144. https://doi.org/10.1080/13658810600894307