多変量クラスター分析の機能

周囲を見渡してみると、物事を組織化、グループ化、区別、分類することによって、それをより深く理解しようとすることが常にごく自然に行われています。このような分類プロセスは、学習と理解の基礎となります。同様に、データをより深く学習し理解するために、[多変量クラスター分析 (Multivariate Clustering)] ツールを使用できます。作成するクラスターの数を指定すると、各クラスター内のすべてのフィーチャはできる限り類似していて、クラスター間はできる限り異質になるような解法を探します。フィーチャの類似性は、[分析フィールド] パラメーターに指定する属性のセットに基づき、クラスターは K 平均アルゴリズムを使用して作成されます。

ヒント:

クラスタリング、グループ化、および分類手法は、機械学習で最も広く使用されている方法です。[多変量クラスター分析 (Multivariate Clustering)] ツールは、教師なし機械学習方法を利用して、データ内の自然なクラスターを決定します。これらの分類方法は、データ内のクラスターを見つけるように方法を誘導およびトレーニングするために、事前に分類されたフィーチャのセットを必要としないため、教師なしであると見なされています。

このようなクラスタリング分析のアルゴリズムは何百もありますが、すべて NP 困難として分類されます。すなわち、グループ内の類似性とグループ間の異質性の両方を完全に最大にする解法を見つけるには、クラスタリングするフィーチャを可能な限り組み合わせてみるしかありません。これは、フィーチャが少数の場合は実行可能ですが、すぐに実行困難になります。

最適な解法を見つけることが困難であるだけでなく、すべての可能なデータのタイプおよびシナリオに最適なクラスタリング アルゴリズムを特定しようとすることは非現実的でもあります。クラスターにはさまざまな形状、サイズ、密度があり、属性データにはさまざまな範囲、対称性、連続性、計測単位が含まれます。そのため、過去 50 年にわたって数多くのクラスター分析アルゴリズムが開発されてきました。ここでは、データ内の基礎となる構造をより深く理解するための予備ツールとして、これらのツールを採用するのが最適です。

適用例

このツールの適用例には、以下のようなものがあります。

• 周辺の農場から取得したサルモネラ菌のサンプルがあり、種類、クラス、場所、日時などの属性がある場合を考えます。細菌が伝染して拡大する様子をより適切に理解するために、[多変量クラスター分析 (Multivariate Clustering)] ツールを使用して、サンプルを個々の「発生」に分割します。解析自体は空間的ではありませんが、結果内の空間パターンを発生の拡大として発見することができます。クラスターが決定したら、[分布指向性分析 (Standard Deviational Ellipse)]、[地理的中心の算出 (Mean_Center)]、または [最近接 (Near)] などの他の空間パターン分析ツールを使用して各発生を解析できます。
• 動物のなわ張りを理解するために動物観察に関するデータを収集した場合、[多変量クラスター分析 (Multivariate Clustering)] ツールが役に立ちます。たとえば、鮭がそれぞれのライフ ステージでいつ、どこに集まってくるのかを知ることは、繁殖を助けるための保護領域を作るのに役立ちます。
• 購買パターン、人口学的特性、移動パターン、またはその他の行動的属性によって顧客をクラスタリングすると、自社製品の有効なマーケティング戦略を立案できます。

入力

このツールは、ポイント、ポリライン、またはポリゴンの [入力フィーチャ]、[出力フィーチャ] のパス、1 つ以上の [分析フィールド]、および作成する [クラスターの数] を表す整数値を受け取ります。[初期化方法] および [クラスターの最適数の評価に使用する出力テーブル] のオプションを含む、複数のオプション パラメーターも存在します。

分析フィールド

スケール率、間隔、等級計測システムを表す数値フィールドを選択します。ダミー (バイナリ) 変数を使用して、名目データを表すことができます。ただし、一般に、これらの変数は他の数値変数タイプのようには機能しません。たとえば、Rural という変数を作成して、各フィーチャ (国勢調査区域など) に対して、農村部である場合は 1、都市部である場合は 0 をそれぞれ割り当てることができます。この変数をさらに適切に表現すると、各フィーチャに関連付けられた農村部の面積または割合になります。

メモ:

ばらつきの多い変数 (データ値が平均値付近で分散する) は、ばらつきの少ない変数よりもクラスターに大きい影響を与える傾向があるため、[分析フィールド] の値がこのツールで標準化されます。属性値の標準化には、Z 変換が含まれます。この変換では、すべての値の平均値を各値から引いた後、その結果をすべての値の標準偏差で割ります。標準化によって、属性が非常に異なる種類の数 (比率 (0 〜 1.0)、人口 (100 万以上)、距離 (キロメートルなど)) で表されている場合でも、すべての属性が同じスケールで表されます。

フィーチャのクラスターを区別する変数を選択する必要があります。たとえば、生徒が受けた標準学力試験の結果をもとに、校区をクラスタリングする場合を考えます。全体の試験得点、数学や国語といった特定科目の結果、試験得点の最低点を満たす生徒の割合などを含む [分析フィールド] を選択できます。[多変量クラスター分析 (Multivariate Clustering)] ツールを実行すると、R² 値が変数ごとに計算されて、メッセージ ウィンドウにレポートされます。たとえば以下のサマリーでは、校区は、生徒の試験得点、その領域で高校を卒業していない大人の割合、生徒 1 人あたりの支出、生徒と教師の平均割合に基づいてグループ化されます。TestScores 変数に最大 R² 値があることに注目してください。これは、この変数により、校区が最も効果的にクラスターに分割されることを示しています。R² 値は、クラスタリング プロセスの後、元の TestScores データのばらつきがどのくらい保持されていたかを表すため、特定の変数の R² 値が大きいほど、その変数はフィーチャを適切に区別します。

詳細:

R² 値は次のように計算されます。

(TSS - ESS) / TSS

ここで、TSS は二乗総和で、ESS は説明された二乗和です。TTS は、変数のグローバル平均値からの偏差を二乗して足したものです。ESS も同じ計算方法で求められますが、クラスターごとの偏差である点が異なります。各値をその値が属しているクラスターの平均値から引いた後、求められた結果を二乗して足します。

クラスターの数

質問または問題に最も適したクラスターの数がわかっている場合は、その数を [クラスターの数] パラメーターに入力します。ただし、多くの場合、特定のクラスター数を選択するための基準はなく、フィーチャの類似性と異質性を最適に区別する数を選択することになります。このような状況に対応するには、[クラスターの数] パラメーターを空白のままにし、[多変量クラスター分析 (Multivariate Clustering)] ツールを使用して、フィーチャを 2 ～最大 30 クラスターに分割したときの有効性を評価します。クラスタリングの有効性は、クラスター間の分散とクラスター内の分散の間の比率である Calinski-Harabasz 疑似 F 統計を使用して計測されます。言い換えると、この比率は、グループ内の類似性およびグループ間の異質性を反映します。

クラスター分析方法

[多変量クラスター分析 (Multivariate Clustering)] ツールは、デフォルトで K 平均アルゴリズムを使用します。K 平均アルゴリズムの目的は、フィーチャを分割し、すべてのクラスターにおいて同じクラスター内のフィーチャ間の異質性を最小にすることです。アルゴリズムは NP 困難であるため、フィーチャのクラスタリングにはグリーディ ヒューリスティックが使用されます。グリーディ アルゴリズムは、常にローカルな最小値に収束しますが、必ずしもグローバルな (最適な) 最小値を見つけるわけではありません。

K 平均アルゴリズムは、各クラスターを拡大させるのに使用されるシードを最初に特定することによって機能します。したがって、シード数は、常に [クラスターの数] に一致します。最初のシードはランダムに選択されます。ただし、ランダム コンポーネントを使用する一方で、その他のシードの選択には、既存のシード フィーチャ セットから最も遠いデータ空間のシードの選択を優先する荷重が適用されます (アルゴリズムのこの部分を K 平均 ++ と呼びます)。[初期化方法] で [最適化されたシード位置] または [ランダムなシード位置] を選択すると、シードの検索にランダム コンポーネントが使用されるため、ツールの実行ごとにクラスタリングの結果が異なる場合があります。

シードが特定されると、すべてのフィーチャは、最近接のシード フィーチャ (データ空間内で最近接) に割り当てられます。フィーチャの各クラスターでは、平均データの中心が計算され、各フィーチャが最近接の中心に再割り当てされます。各クラスターの平均データの中心を計算して、フィーチャを最近接の中心に再割り当てする処理は、クラスターのメンバーシップが安定するまで続けられます (反復の最大数は 100)。

K 平均アルゴリズムと同様に、K-Medoids 法は、各クラスターを拡大させるのに使用されるシード フィーチャを最初に特定することによって機能します。各シード フィーチャは、[入力フィーチャ] の実際のフィーチャです。これらのシード フィーチャは medoid (メドイド) と呼ばれます。すべてのフィーチャは、最近接の medoid (データ空間内で最近接) に割り当てられます。これが初期のクラスター解です。medoid とすべての非 medoid フィーチャの間の (データ空間内の) 距離の合計が計算されます。この入れ替えによって距離の合計が増えた場合、入れ替えられたフィーチャが新しい medoid になります (合計が増えなかった場合、入れ替えは取り消されます)。この入れ替えによって距離の合計が増えた場合、入れ替えられたフィーチャが新しい medoid になります (合計が増えなかった場合、入れ替えは取り消されます)。新しい medoid を探して、フィーチャを最近接の medoid に再割り当てする処理は、クラスターのメンバーシップが安定するまで続けられます。

K 平均と K Medoids はいずれも一般的に使用されるクラスター分析アルゴリズムで、ほとんどの場合同様の結果になります。ただし、K Medoids のほうが、[入力フィーチャ] のノイズと外れ値に対してより頑健です。K 平均は一般に K Medoids より短時間で分析でき、大規模なデータ セットに適しています。

出力

[多変量クラスター分析 (Multivariate Clustering)] ツールでは、数多くの出力が作成されます。これらのメッセージには、[ジオプロセシング] ウィンドウからアクセスできます。そのためには、プログレス バーの上にカーソルを置くか、ツールの進行状況ボタン をクリックするか、[ジオプロセシング] ウィンドウの下部にあるメッセージ セクションを展開します。ジオプロセシング履歴を介して、以前に実行した [多変量クラスター分析 (Multivariate Clustering)] のメッセージにアクセスすることもできます。

[多変量クラスター分析 (Multivariate Clustering)] ツールのデフォルトの出力は、分析で使用されるフィールドと、各フィーチャがどのクラスターに属するかを特定する CLUSTER_ID と呼ばれる新しい整数フィールドを含む、新しい出力フィーチャクラスです。この出力フィーチャクラスは、CLUSTER_ID フィールドに適用される固有のカラー レンダリング スキーマによって、コンテンツ ウィンドウに追加されます。IS_SEED フィールドには、クラスターを拡大させるシードとして選択されて使用されたフィーチャが示されます。

[多変量クラスター分析 (Multivariate Clustering)] の結果の例

[多変量クラスター分析 (Multivariate Clustering)] のチャート出力

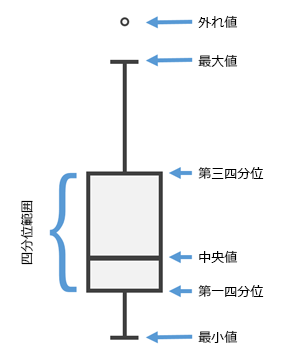
作成されたクラスターを集計するために、複数のタイプのチャートが作成されます。[箱ひげ図] は、各クラスターの特徴および解析で使用された各変数の特徴の両方に関する情報を示すために使用されます。下の図は、作成された [分析フィールド] およびクラスターごとの箱ひげ図およびそれらのサマリー値 (最小データ値、第 1 四分位値、グローバル中央値、第 3 四分位値、最大データ値、およびデータの外れ値 (四分位範囲よりも 1.5 倍小さい、または大きい値)) を解釈する方法を示しています。 これらの値および四分位範囲の値を確認するには、チャート上の箱ひげ図の上にポインターを置きます。最小値または最大値 (上または下のひげ) の外側にあるポイント マークは、データの外れ値を表します。

詳細:

四分位範囲 (IQR) は、第 3 四分位から第 1 四分位を引いたものです。 下の外れ値は 1.5 * IQR よりも小さい値 (Q1 - 1.5 * IQR) で、上の外れ値は 1.5 * IQR よりも大きい値 (Q3 + 1.5 * IQR) です。外れ値は、箱ひげ図ではポイント シンボルで表示されます。

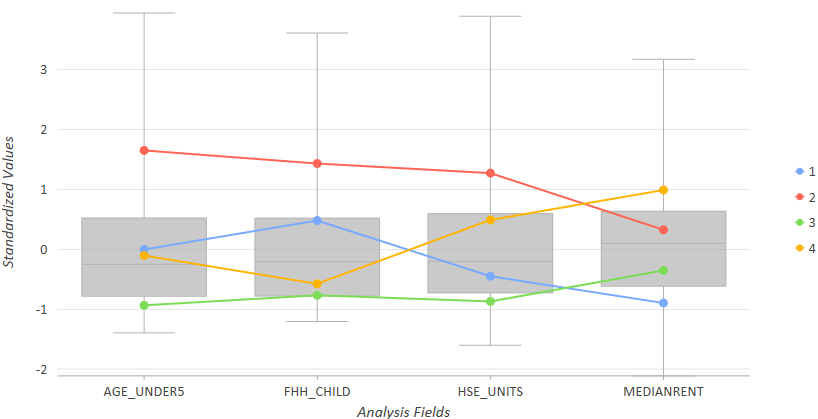
デフォルトの平行箱ひげ図では、クラスターと変数の両方の概要が表示されます。たとえば、[多変量クラスター分析 (Multivariate Clustering)] ツールが国勢調査地区に対して実行され、4 つのクラスターが作成されました。次のチャートから、クラスター 2 (赤) は、他のクラスターと比べて平均以上の賃貸料、母子家庭世帯数 (FHH_CHILD) の最大値、住戸数 (HSE_UNITS) の最大値、5 歳未満の子供の数の最大値を含む区域を表していることがわかります。クラスター 4 (鮮やかな黄色) は、賃貸料の最大中央値、母子家庭世帯数のほぼ最小値、および平均値を上回る住戸数を含む区域を表しています。クラスター 3 (緑) は、母子家庭世帯数の最小値、5 歳未満の子供の数の最小値、住戸数の最小値、および賃貸料のほぼ最低値 (ただし、クラスター 1 ほどは低くない) を含む区域を表しています。[分析フィールド] ごとのクラスターの平均値を確認するには、平均ラインの各ノードの上にポインターを置きます。

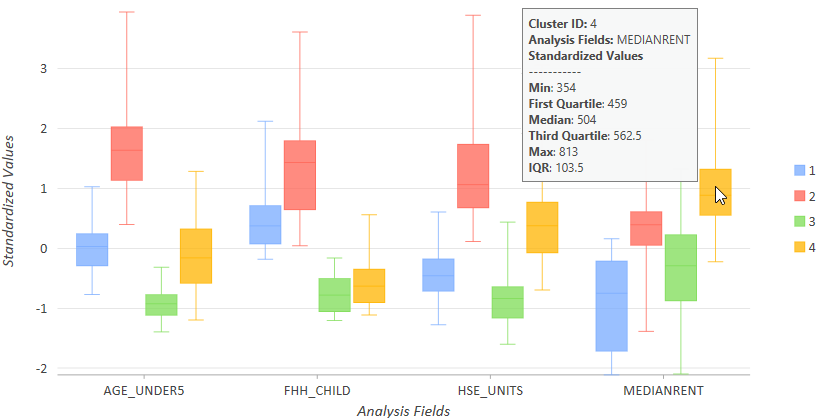
上の平行箱ひげ図を使用して解析のグローバル サマリーを調べた後に、[チャート プロパティ] ウィンドウの [シリーズ] タブで [並べて表示] に切り替えることによって、変数ごとに各クラスターの箱ひげ図を調べることができます。このデータ表示では、どのグループに各変数内の値の最大と最小の範囲があるかが容易にわかります。箱ひげ図は、各変数についてクラスターごとに作成されるため、各クラスターの値が作成された他のクラスターにどのように関連しているかを確認することができます。各クラスター内の変数ごとの最小値、最大値、および中央値を確認するには、各変数の箱ひげ図の上にポインターを置きます。たとえば、下のチャートでは、クラスター 4 (鮮やかな黄色) に MEDIANRENT 変数の最大値が存在し、354 ～ 813 の範囲の値を持つ区域が含まれていることがわかります。

クラスターあたりのフィーチャ数を示すバー チャートも作成されます。各バーを選択すると、マップ内のクラスターのフィーチャも選択されます。この機能は、さらに解析する場合に役立つことがあります。

[クラスターの数] パラメーターを空のままにした場合、このツールはデータに基づいてクラスターの最適数を評価します。[クラスター数の評価に使用する出力テーブル] のパスを指定した場合、計算された疑似 F 統計値を示すチャートが作成されます。グラフ上の最高のピークが最大 F 統計量で、指定したフィーチャと変数を最も効果的に区別するクラスターの数を示します。以下のチャートでは、4 つのグループに関連付けられた F 統計量が最大です。疑似 F 統計量の高い 5 つのグループを選択してもかまいません。

クラスターの最適数を評価するための疑似 F 統計チャート

ベスト プラクティス

可能な限り多くの [分析フィールド] を含めたい傾向がありますが、[多変量クラスター分析 (Multivariate Clustering)] ツールは単一の変数およびビルドで開始することにより最適に機能します。分析フィールドの数が少ないほうが、結果の解析が容易になります。また、フィールドの数が少ないと、どの変数が最適な区別を実行するか判断しやすくなります。

多くのシナリオでは、[多変量クラスター分析 (Multivariate Clustering)] ツールを何度も実行して、最適な [クラスターの数]、およびフィーチャをクラスターに最適に分類する [分析フィールド] の最も効果的な組み合わせを探すことになります。

このツールがクラスターの最適数として 30 を返した場合、F 統計量のチャートを必ず調べてください。クラスターの数を選択して F 統計量のチャートを解釈することは、高度な技術を要し、クラスターの数が少ないほど、解析により適している場合があります。

参考資料

Jain, A. K. 2009. 「Data Clustering: 50 years beyond K-Means」 Pattern Recognition Letters

Hinde, A., T. Whiteway, R. Ruddick, and A. D. Heap. 2007. 「Seascapes of the Australian Margin and adjacent sea floor: Keystroke Methodology」Geoscience Australia, Record 2007/10, 58pp