需要 Geostatistical Analyst 许可。
克里金法依赖于数学和统计模型。 添加包含概率的统计模型可以区分克里金法和空间插值的确定性方法中描述的确定性方法。 对于克里金法,需要将某种概率与预测相关联;也就是说,无法通过统计模型完美地预测这些值。 考虑在田地中测量氮值样本的示例。 显然,即使样本很大,您也无法预测某些未测量位置处的氮的确切值。 因此,您不仅需要尝试进行预测,而且还需要评估预测的误差。
克里金法依赖于自相关的概念。 相关性通常被认为是两种变量之间相关的趋势。 例如,股票市场往往在利率较低时出现上涨,因此认为两者负相关。 但是,股票市场呈现正自相关性,这意味着其本身具有相关性。 在股票市场中,如果两个数值仅相隔一天,则其往往比相隔一年时更加相似。 这与地理学的基本原理有关:距离较近的事物往往比较远的事物更加相似。 可将相关性衰减的速率表示为距离的函数。
自相关是距离的函数。 这是地统计学的一个决定性特征。 在经典统计学中,假定观测点相互独立,即,观测点之间不存在相关性。 在地统计学中,空间位置信息用于计算观测点之间的距离,并将自相关性建模为距离的函数。
还需注意,一般来说,股票市场会随着时间的推移而上涨,这就是所谓的趋势。 对于地统计数据,这些术语同样适用,其数学表达如下述简单公式所示:
Z(s) = µ(s) + ε(s),其中 Z(s) 为感兴趣变量,分解为确定性趋势 µ(s) 和随机自相关误差形式 ε(s)。 符号 s 用于指示位置;可将其视为包含空间 x(经度)和 y(纬度)坐标。 此公式的变体构成所有不同类型克里金法的基础。 从右侧开始,然后向左移动。
无论模型中的趋势多么复杂,µ(s) 仍然无法完美地预测。 在这种情况下,需要对误差项 ε(s) 进行一些假设;即,您期望其为 0(平均值),并且 ε(s) 和 ε(s + h) 之间的自相关不取决于实际位置 s,而仅取决于两者之间的位移 h。 这是确保结果可重复性的必要步骤,以便据此估算自相关函数。 例如,在下图中,假定箭头所连接位置对处的随机误差具有相同的自相关性:
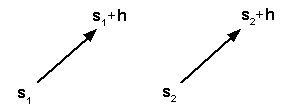
接下来,检查趋势。 它可以是一个简单的常数,即对于所有位置 s,均有 µ(s) = m,如果 µ 未知,则为普通克里金法所基于的模型。 它也可以由空间坐标本身的线性函数组成,例如:
µ(s) = ß0 + ß1x + ß2y + ß3x2 + ß4y2 + ß5xy,这是一个二阶多项式趋势表面,并且只是空间 x 和 y 坐标的线性回归。 对于随时间变化且回归系数未知的趋势,可构建泛克里金法模型。 如果趋势完全已知(即所有参数与协变量均已知),则无论其是否恒定,均可构建简单克里金法模型。
现在,查看分解的左侧:Z(s) = µ(s) + ε(s)。 可以对 Z(s) 执行变换。 例如,可以将其更改为指示变量,如果 Z(s) 低于某个值(例如,臭氧浓度为 0.12 ppm),则为 0;如果高于某个值,则为 1。 您可能希望预测 Z(s) 高于阈值的概率,并且基于此模型的预测构建指示克里金法。 可以对 Z(s) 进行常规未指定变换,并将其称为第 i 个变量的 fi(Z(si))。 可以构建变量函数的预测因子;例如,如果您希望在位置 s0 处进行预测,则可以使用数据 fi(Z(si)) 构建 g(Z(s0)) 的析取克里金法预测因子。
最后,考虑存在多个变量类型的情况,并且为第 j 个变量类型构建模型 Zj(s) = µj(s) + εj(s)。 由此,可以考虑每个变量的不同趋势,除了误差 εj(s) 的自相关之外,您也可以考虑两种变量类型的误差 εj(s) 和 εk(s) 之间的互相关。 例如,可以考虑臭氧浓度和颗粒物浓度这两个变量之间的互相关性,并且其测量位置无需完全一致。 基于多个感兴趣变量的模型构成了协同克里金法的基础。 可以构建 Z(s) 的指示变量,并且如果在协同克里金法模型中使用原始未转换数据 Z(s) 进行预测,则可以得到概率克里金法。 如果涉及多个感兴趣变量,则可将普通协同克里金法、泛协同克里金法、简单协同克里金法、指示协同克里金法、概率协同克里金法和析取协同克里金法视为前文所述各类克里金法的多变量扩展形式。