Das Werkzeug Raten berechnen berechnet verschiedene Raten. Das Werkzeug berechnet Prozentsätze, Verhältnisse, Inzidenzraten oder geglättete Raten. Geglättete Raten können mit einer der folgenden Methoden berechnet werden: globale empirische Bayes-Rate, lokale empirische Bayes-Rate, lokal gewichtete Durchschnittsrate oder lokal gewichtete Medianrate.
Die Methode "Bruttorate" kann zur Berechnung von Prozentsätzen, Verhältnissen und Inzidenzraten verwendet werden. Für Features mit einer geringen Anzahl oder Grundgesamtheit ist jedoch die Glättungsmethode besser geeignet. Die Glättungsmethoden verwenden Informationen der räumlichen Nachbarn eines Features oder einer Referenzrate, um die Bruttorate für jedes Feature anzupassen. Das Werkzeug enthält die folgenden Glättungsmethoden:
- Globale empirische Bayes-Rate: Passt die Bruttorate jedes Features an eine globale Referenzrate an. Der Grad der Anpassung wird durch die Größe der Grundgesamtheit des Features beeinflusst. Verwenden Sie diese Option, wenn Sie der Meinung sind, dass ein konstantes Grundrisiko für alle Features besteht.
- Lokale empirische Bayes-Rate: Passt die Bruttorate jedes Features an eine lokale Referenzrate an. Verwenden Sie diese Option, wenn Sie der Meinung sind, dass eine räumliche Variabilität bezüglich des Risikos gegeben ist.
- Lokal gewichtete Durchschnittsrate: Legt die Rate jedes Features auf Basis der gewichteten Durchschnittsrate seiner Nachbarschaft fest.
- Lokal gewichtete Medianrate: Legt die Rate jedes Features auf Basis der gewichteten Medianrate seiner Nachbarschaft fest.
Potenzielle Anwendungsbereiche
Raten werden in den folgenden Situationen berechnet:
- Berechnen einfacher Prozentwerte. Beispielsweise der Prozentsatz der Personen in der Erwerbsbevölkerung, die arbeitslos sind.
- Berechnen von Verhältnissen. Zum Beispiel das Verhältnis von Frauen und Männern in jedem Landkreis.
- Berechnen von Inzidenzraten. Zum Beispiel die Rate von Speiseröhrenkrebs bei Frauen. Diese Rate ist eine Schätzung der Wahrscheinlichkeit, dass in einem bestimmten Zeitraum ein Ereignis pro Person in der Grundgesamtheit auftritt. Sie stellt die Wahrscheinlichkeit dar, dass für eine nach dem Zufallsprinzip ausgewählte Person in dieser Grundgesamtheit das Ereignis in dem Zeitraum auftritt. In diesem Szenario ist die Rate eine Zahl zwischen 0 und 1, und die Anzahl ist eine Teilmenge der Personen in der Grundgesamtheit.
- Es wird die Intensität des Vorkommens eines Ereignisses relativ zu einer Bezugseinheit gemessen. Zum Beispiel die Intensität der im Jahre 2020 geposteten Tweets pro Person. In diesem Fall kann die Rate höher als 1 sein, da die Anzahl nicht unbedingt eine Teilmenge der Grundgesamtheit sein muss.
Zugrunde liegende Konzepte
Das Werkzeug Raten berechnen berechnet Raten mit einer der folgenden Methoden: Bruttorate, Globale empirische Bayes-Rate, Lokale empirische Bayes-Rate, Lokal gewichtete Durchschnittsrate oder Lokal gewichtete Medianrate. Die Methode "Bruttorate" ist die einfachste aller Methoden. Sie berechnet das Verhältnis zwischen der Anzahl eines Ereignisses und der Grundgesamtheit in einem bestimmten Zeitraum.
Um zum Beispiel die Kindersterblichkeitsrate zu verstehen, können Sie Ihre Analyse mit der Methode der Bruttorate beginnen, um ein einfaches Verhältnis zu berechnen. Im folgenden Diagramm wird die Rate der Kindersterblichkeit für 728 räumliche Features dargestellt, indem die Anzahl der Kindstode im Jahre 2020 durch die Gesamtzahl der im Jahre 2020 geborenen Kinder dividiert wird. Die Daten umfassen einige Großstädte sowie zahlreiche Kleinstädte. Die Größe der Grundgesamtheit und die Zahl der geborenen Kinder variieren je nach räumlichem Feature erheblich.
Im Diagramm weisen die Raten eine hohe Variabilität auf, wenn die Anzahl der geborenen Kinder gering ist, und eine relativ niedrige Variabilität, wenn die Anzahl der geborenen Kinder hoch ist. Für Gebiete mit weniger als 100 Geburten pro Jahr reichen die Raten von 0 (der kleinste mögliche Wert) bis 0,20. Selbst in verarmten Regionen weltweit gibt es keine geschätzte Kindersterblichkeitsrate von 0,20 bzw. 2 Kindstode pro 10 geborenen Kindern. In Gebieten mit mindestens 1.000 Geburten gibt es hingegen keine Raten unter 0,02 oder über 0,08. Dies könnte darauf hindeuten, dass die Kindersterblichkeitsraten in Gebieten mit kleineren Grundgesamtheiten höher sind. Die Hauptursache ist jedoch die größere Varianz der Raten in kleinen Gebieten, die bewirkt, dass die Raten weniger zuverlässig als die Raten für Regionen mit größeren Bevölkerungszahlen sind.
Die größere Variabilität wird durch die äußerst starke Empfindlichkeit der Raten gegenüber der Bevölkerungsgröße verursacht, und nicht durch die tatsächlichen Unterschiede bei den Sterbewahrscheinlichkeiten in den Gebieten. Dieses Problem hängt mit dem so genannten Problem der kleinen Zahlen zusammen. Das Problem der kleinen Zahlen tritt immer dann auf, wenn Sie Prozentsätze, Verhältnisse, Proportionen oder Raten für geographische Bereiche berechnen, in denen die Bevölkerung dünn besiedelt ist oder in denen das Ereignis selten auftritt. In diesen Szenarien können kleine zufällige Schwankungen der Ereignisanzahl zu großen Schwankungen der resultierenden Ratenwerte führen. Im vorigen Beispiel wiesen 15 Gebiete weniger als 30 Geburten und keinen Todesfall auf. Käme es in diesen Gebieten zu einem einzigen Todesfall, würden die Raten steil von 0 auf einen Wert zwischen 0,05 und 0,42 ansteigen (dies entspräche einer Sterblichkeitsrate von 42 Prozent).
Beim Berechnen von Raten möchten Sie die räumliche Varianz der Ereigniswahrscheinlichkeit oder in diesem Beispiel der Kindersterblichkeit ermitteln. Die Variation der Bruttoraten wird jedoch zum Teil durch Schwankungen verursacht, die nicht mit der zugrunde liegenden Ereigniswahrscheinlichkeit zusammenhängen. Diese Variation ist für Features mit kleineren Grundgesamtheiten größer. Dadurch sind die entsprechenden Raten weniger zuverlässig als die für Features mit größeren Grundgesamtheiten berechneten Raten. Um diese Beschränkung der Methode "Bruttorate" zu vermeiden, können Sie eine der zusätzlichen Berechnungsmethoden verwenden, die das Werkzeug Raten berechnen enthält.
Die Methoden "Lokale empirische Bayes-Rate" und "Globale empirische Bayes-Rate" behandeln die Variabilität bei den Bruttoraten von Features mit kleiner Grundgesamtheit, indem die Bruttorate jedes Features an eine Referenzrate angepasst wird. Der Grad der Anpassung hängt von der Größe der Grundgesamtheit ab: Bei größeren Grundgesamtheiten ist die Änderung zwischen der geschätzten Bruttorate und der geschätzten empirischen Bayes-Rate minimal, während bei kleineren Grundgesamtheiten deutlichere Anpassungen erfolgen.
Weitere Informationen zur globalen empirischen Bayes-Rate
Weitere Informationen zur lokalen empirischen Bayes-Rate
Die Methoden "Lokal gewichtete Durchschnittsrate", "Lokal gewichtete Medianrate" und "Lokale empirische Bayes-Rate" wenden zum Berechnen der Raten räumliche Glättung an. Die Rate jedes Features wird anhand der Rate seiner Nachbarschaft berechnet. Wenn die Nachbarn und Gewichtungen der Nachbarn jedes Features ermittelt wurden, werden die Feature-Raten mit dem Parameter Ratenmethode berechnet. Jedes Feature weist einen der folgenden Typen von Raten auf:
- Lokal gewichtete Durchschnittsrate: Die gewichtete Durchschnittsrate der Nachbarschaft des Features.
Weitere Informationen zu "Lokal gewichtete Durchschnittsrate"
- Lokal gewichtete Medianrate: Die gewichtete Medianrate der Nachbarschaft des Features.
Werkzeugeingaben
Das Werkzeug enthält mehrere Parameter zum Definieren und Konfigurieren der Raten.
Ratenfelder
Der Parameter Ratenfelder gibt die Felder an, die zum Berechnen der Raten verwendet werden. Der Parameter enthält einen Zählfeld-Wert, der das Feld im Eingabe-Layer mit der Ereignisanzahl angibt, und einen Wert für Feld mit Grundgesamtheit, der das Feld in der Eingabe mit Daten zur Grundgesamtheit angibt, das dem ausgewählten Zählfeld entspricht.
Sie können eine einzelne Rate oder mehrere Raten berechnen. Geben Sie zum Berechnen mehrerer Raten mehrere Werte für Zählfeld und Feld mit Grundgesamtheit an. Wenn z. B. die Feature-Class ein Feld für die Anzahl der Krebstodesfälle in den Jahren 2014, 2020 und 2024 und ein Feld für die Grundgesamtheit für diese Jahre enthält, können Sie drei Krebstodesraten berechnen. Wenn Sie mehrere Raten berechnen, werden zum Berechnen der einzelnen Raten die für Ratenmethode und Ratenmultiplikator angegebenen Parameterwerte angewendet.
Ratenmethode
Der Parameter Ratenmethode gibt die Methode an, die zum Berechnen der Raten verwendet wird.
Bruttorate
Die geschätzte Bruttorate wird wie folgt berechnet:
wobei ri die Bruttorate, ni die Grundgesamtheit und Yi die Anzahl im iten räumlichen Feature bezeichnet. Die Bruttorate wird für jedes Feature berechnet. Features mit einer geringeren Anzahl als null oder einer Grundgesamtheit kleiner oder gleich null erhalten jedoch die Rate NULL. Mit den Feldern Confidence interval- upper 95%, Confidence interval- lower 95% und Reliable in der Ausgabe-Feature-Class oder Ausgabetabelle können Sie die Zuverlässigkeit jeder Schätzung der Bruttorate bewerten. Wenn viele Features große Konfidenzintervalle oder hohe Zuverlässigkeitswerte aufweisen, sollten Sie möglicherweise eine andere Ratenmethode verwenden.
Globale empirische Bayes-Rate
Die Methode "Globale empirische Bayes-Rate" schätzt die Raten anhand des gewichteten Durchschnitts der Bruttorate und einer Referenzrate. Die Berechnung mit der Methode lautet wie folgt:
wobei i das räumliche Feature, 
die geschätzte globale empirische Bayes-Rate, Ci eine Gewichtung zwischen 0 und 1, 
die geschätzte Bruttorate des Features i und 
die Referenzrate ist.
Die Referenzrate ist die Durchschnittsrate aller Features. Die Referenzrate wird berechnet, indem die Summe jeder Anzahl von Features durch die Summe aller Feature-Grundgesamtheiten wie folgt dividiert wird:
wobei die Referenzrate, Yi die Grundgesamtheit des iten Features und ni deren Anzahl ist. Die Gewichtung Ci variiert zwischen Features und wird durch die Größe der Grundgesamtheit des Features beeinflusst. Wenn ein Feature eine große Grundgesamtheit aufweist, ist die Gewichtung nahezu 1, und die Schätzung der globalen empirischen Bayes-Rate eines Features ist mit seiner geschätzten Bruttorate fast identisch. Wenn die Grundgesamtheit klein ist, sinkt die Bruttorate in Richtung der Referenzrate, da die Gewichtung Ci kleiner als 1 ist. In diesem Fall ist die Schätzung der globalen empirischen Bayes-Rate der gewichtete Durchschnitt der Bruttorate und Referenzrate.
Wenn der Parameter Ratenmethode auf Globale empirische Bayes-Rate oder Lokale empirische Bayes-Rate festgelegt ist, müssen Sie außerdem einen Wert für den Parameter Wahrscheinlichkeitsverteilung angeben. Die Wahrscheinlichkeitsverteilung ist die Verteilung, von der angenommen wird, dass sie die beobachteten Werte für die Anzahl abbildet. Der Parameter Wahrscheinlichkeitsverteilung umfasst zwei Optionen: Poisson und Binomial. Die Standardoption ist Poisson, eine häufig verwendete Verteilung für die Modellierung von Raten. Diese Option kann verwendet werden, wenn die Intensität oder Wahrscheinlichkeit des Vorkommens eines Ereignisses geschätzt wird. Das Modell der Binomialwahrscheinlichkeitsverteilung basiert auf den folgenden Voraussetzungen:
- Die Ereignisanzahl (Zähler) ist eine Teilmenge der Grundgesamtheit (Nenner).
- Jedes Ereignis ist von den anderen Ereignissen unabhängig.
- Die Wahrscheinlichkeit, dass ein Ereignis auftritt, ist für jedes Ereignis gleich.
Wenn eine dieser Voraussetzungen nicht erfüllt wird, ist die Binomialverteilung kein geeignetes Modell. Es wird empfohlen, die Binomialverteilung nur dann zu wählen, wenn diese Voraussetzungen erfüllt sind und die Wahrscheinlichkeit des Ereignisses nicht gering ist.
Lokale empirische Bayes-Rate
Die Schätzung der lokalen empirischen Bayes-Rate eines Features ist der gewichtete Durchschnitt der Bruttorate des fokalen Features und der gewichteten Durchschnittsrate seiner Nachbarschaft. Die lokale empirische Bayes-Rate wird wie folgt berechnet:
wobei i das betrachtete Feature, 
die Schätzung der lokalen empirischen Bayes-Rate, Ci die Gewichtung,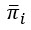 
die gewichtete Durchschnittsrate des Features i und seiner Nachbarn und die Bruttorate des fokalen Features ist.
Die Durchschnittsrate der Nachbarschaft eines Features 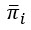wird durch die Werte der Parameter Nachbarschaftstyp und Lokales Gewichtungsschema bestimmt. Der Parameter Nachbarschaftstyp gibt die Methode an, mit der die Nachbarn der einzelnen Features bestimmt werden. Jedem Nachbarn wird eine auf dem Wert des Parameters Nachbarschaftstyp oder Lokales Gewichtungsschema basierende Gewichtung zugewiesen. Das Werkzeug berechnet dann die lokal gewichtete Durchschnittsrate jeder Nachbarschaft wie folgt:
wobei i das betrachtete Feature, 
die lokal gewichtete Durchschnittsrate bei i, j der Nachbar, wij die Gewichtung des Nachbarn j und 
die geschätzte Bruttorate des Nachbarn j ist.
Lokal gewichtete Durchschnittsrate
Die Methode "Lokal gewichtete Durchschnittsrate" schätzt die Rate eines Features, indem die gewichtete Durchschnittsrate seiner Nachbarschaft berechnet wird. Für die Schätzung der lokal gewichteten Durchschnittsraten wendet das Werkzeug zunächst den Wert des Parameters Nachbarschaftstyp an, um die Nachbarn der einzelnen Features zu ermitteln. Anschließend wird jedem Nachbarn eine auf dem Wert des Parameters Nachbarschaftstyp oder Lokales Gewichtungsschema basierende Gewichtung zugewiesen. Dann wird die lokal gewichtete Durchschnittsrate jedes Features wie folgt berechnet:
wobei i das betrachtete Feature, die lokal gewichtete Durchschnittsrate bei i, j der Nachbar, wij die Gewichtung des Nachbarn j und die geschätzte Bruttorate des Nachbarn j ist.
Lokal gewichtete Medianrate
Die Methode "Lokal gewichtete Medianrate" schätzt die Rate eines Features, indem die gewichtete Medianrate seiner Nachbarschaft berechnet wird.
Lokale Methoden
Die lokalen Methoden verwenden die Nachbarn eines Features, um seine Rate zu schätzen. Nachbarn werden auf Grundlage des unter Nachbarschaftstyp angegebenen Parameterwertes identifiziert, und dann wird jedem Nachbar eine Gewichtung zugewiesen.
Weitere Informationen zu Nachbarschaftstypen
Nachbargewichtungen können mithilfe einer geographischen Gewichtungsfunktion (Kernel-Funktion) aufgehoben oder berechnet werden. Der Parameter Lokales Gewichtungsschema unterstützt folgende Optionen für die Nachbarschaftsgewichtung: Ungewichtet, Gauß und Biquadrat. Verwenden Sie das Gewichtungsschema, das am besten wiedergibt, wie sich die Anzahl der Nachbarereignisse auf die Anzahl der Ereignisse eines fokalen Features auswirkt. Wenn alle Nachbarn das fokale Feature beeinflussen, sollten Sie unabhängig von der Entfernung die Option Ungewichtet verwenden.
Wenn der Einfluss von Nachbarn von der Entfernung abhängt, sollten Nachbarn, die weiter von dem fokalen Feature entfernt sind, weniger Gewichtung erhalten und einen geringeren Einfluss auf die geschätzte Rate des fokalen Features haben. Nachbarn, die näher an dem fokalen Feature liegen, sollten eine höhere Gewichtung erhalten und einen größeren Einfluss auf die geschätzte Rate haben. Wählen Sie in diesem Fall die Option Gauß oder Biquadrat. Mit diesen Optionen werden die Gewichtungen mithilfe eines Kernels ermittelt. Dies ist eine Funktion, die bestimmt, wie schnell die Gewichtung mit zunehmender Entfernung abnimmt. Bei beiden Optionen wird dem fokalen Feature eine Gewichtung von 1 zugewiesen, und wird die Gewichtung in dem Maße allmählich reduziert, in dem die Entfernung vom fokalen Feature zunimmt. Im Vergleich zu einem Gauß-Gewichtungsschema nehmen die Gewichtungen in einem Biquadrat-Gewichtungsschema mit den gleichen Nachbarschaftsspezifikationen schneller ab.
Bei Gauß oder Biquadrat müssen Sie auch den Parameter Kernel-Bandbreite festlegen. Legen Sie eine geeignete Kernel-Bandbreite basierend auf Ihren Daten fest. Wenn Sie hier keinen Wert angeben, wird ein Standardwert geschätzt.
Ratenmultiplikator
Jede Rate ist ein Wert zwischen 0 und 1. Wenn die Grundgesamtheit groß oder das betrachtete Ereignis selten ist, sind die resultierenden Raten gering. Die Raten enthalten viele führende Nullen, und dies kann die Interpretation der Raten erschweren. Der Parameter Ratenmultiplikator ist ein ganzzahliger Wert, der die Raten skaliert, damit sie leichter zu interpretieren und aussagekräftiger sind. Durch Festlegen des Raten-Multiplikators auf 100 wird ein Prozentsatz berechnet. Als Faustregel gilt, dass zum Bestimmen des Ratenmultiplikators der kleinste Ratenwert verwendet werden sollte. Wenn z. B. die kleinste Rate drei führende Nullen aufweist, sollte der Wert von Ratenmultiplikator 10.000 oder höher sein. Die kleinste Rate, die nicht 0 ist, wird dann größer als 1 sein.
Wenn Sie den Wert Ratenmultiplikator festlegen, werden die Raten als die erwartete Anzahl pro Ratenmultiplikatoreinheiten ausgedrückt. Wenn Sie zum Beispiel die Todesraten bei Bauchspeicheldrüsenkrebs berechnen und den Wert Ratenmultiplikator auf 100.000 festlegen, geben die resultierenden Raten die erwartete Anzahl pro 100.000 Personen an. Ein Feature mit einer Rate von 144 würde bedeuten, dass für jede Gruppe von 100.000 Menschen 144 Todesfälle aufgrund von Bauchspeicheldrüsenkrebs pro Jahr zu erwarten sind.
Werkzeugausgaben
Das Werkzeug erzeugt eine Ausgabetabelle oder Ausgabe-Feature-Class, einen Ausgabe-Gruppen-Layer und Geoverarbeitungsmeldungen.
Ausgabe-Features oder -Tabelle
Die Ausgabe-Feature-Class oder Ausgabetabelle enthält mehrere Felder.
Überschussrate
Das Feld Excess Rate vergleicht die Rate eines Features mit der Durchschnittsrate aller Features. Die Überschussrate wird berechnet, indem die beobachtete Rate eines Features durch die Durchschnittsrate aller Features dividiert wird. Die Überschussrate kann jeden positiven Wert größer oder gleich null aufweisen. Werte der Überschussrate nahe 1 bedeuten, dass die geschätzte Rate der Durchschnittsrate entspricht. Wenn die Überschussrate kleiner als 1 ist, ist die geschätzte Rate des Features kleiner als die Durchschnittsrate. Wenn die Überschussrate größer als 1 ist, ist die geschätzte Rate des Features größer als die Durchschnittsrate. Beispielsweise ist die Rate eines Features mit einer Überschussrate von 1,25 um 25 Prozent höher als die Durchschnittsrate. Wenn hingegen die Überschussrate eines Features 0,75 beträgt, ist dessen Rate 25 Prozent niedriger als die Durchschnittsrate.
Standardisierte Rate
Das Feld Standardized Rate gibt an, wie stark die Rate eines Features von der mittleren Rate abweicht. Die standardisierte Rate wird wie folgt berechnet:
wobei z die standardisierte Rate, 
die geschätzte Rate, die mittlere Rate und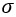 
die Standardabweichung ist. Die Raten von Features mit negativer standardisierter Rate sind kleiner als die mittlere Rate. Die Raten von Features mit positiver standardisierter Rate sind größer als die mittlere Rate. Je größer der negative Wert einer standardisierten Rate, desto stärker ihre negative Abweichung vom Mittelwert. Je größer der positive Wert einer standardisierten Rate, desto stärker ihre positive Abweichung vom Mittelwert. Features, deren standardisierte Raten größer als 3 oder kleiner als -3 sind, gelten als Ausreißer.
Konfidenzintervalle
Wenn der Wert des Parameters Ratenmethode auf Bruttorate festgelegt ist, enthält die Ausgabetabelle oder -Feature-Class die Felder Confidence Interval – Upper 95% und Confidence Interval- Lower 95%. Das 95-Prozent-Konfidenzintervall wird mit der vom Center for Disease Control (CDC) des National Center for Health Statistics empfohlenen Methodik berechnet. Wenn die Anzahl eines Features größer oder gleich 100 ist, empfiehlt sich eine Gauß-Approximation, und das resultierende 95-Prozent-Konfidenzintervall für die Bruttorate wird wie folgt berechnet:
wobei ri die Bruttorate und Yi die Anzahl ist.
Wenn die Anzahl kleiner als 100 ist, wird das 95-Prozent-Konfidenzintervall mit einer Methode berechnet, die von K. Ulm in A simple method to calculate the confidence interval of a standardized mortality ratio (SMR) empfohlen wird. In diesem Fall ist die Gauß-Approximation der Poisson-Verteilung ungeeignet. Stattdessen wird eine Identität zwischen Wahrscheinlichkeiten nach einer Poisson-Verteilung und der Chi-Quadrat-Verteilung verwendet. Angenommen, qgamma(p,x) stellt das Quantil dar, das der Wahrscheinlichkeit p einer Gamma-Verteilung mit dem Formparameter x und dem Ratenparameter 1 zugeordnet ist. Dann wird das 95-Prozent-Konfidenzintervall wie folgt berechnet:
Zuverlässig
Die Werte im Feld Reliable geben die Zuverlässigkeit der Ratenschätzung wieder. Dieses Feld ist im Ausgabe-Feature oder in der Ausgabetabelle enthalten, wenn der Wert des Parameters Ratenmethode auf Bruttorate festgelegt ist. Die Berechnung entspricht der Methode, die im Referenzhandbuch des CDC (Center for Disease Control and Prevention) beschrieben ist. Wenn der Wert von "Zuverlässig" groß ist, ist die Schätzung der Bruttorate ungenau, und die Bruttorate gilt als unzuverlässig. Seit dem Jahre 1989 betrachtet das CDC in den Statistiken des National Center for Health Statistics jede Bruttorate, die auf einer Anzahl von weniger als 20 basiert, als statistisch unzuverlässig. Dies entspricht einem Zuverlässigkeitswert von größer oder gleich 22,94.
Die Zuverlässigkeit wird mit dem relativen Standardfehler (RSF) berechnet, der auch als Variationskoeffizient bezeichnet wird. Der RSF ist das mit 100 multiplizierte Verhältnis zwischen dem Standardfehler der Rate und der geschätzten Rate. Die Ratenvarianz wird wie folgt berechnet:
in Kombination mit der Annahme einer Anzahl ungleich Null führt die RSF-Berechnung wie folgt durch:
Der RSF hängt nur von der Anzahl (Yi) ab. Die Berechnung des RSF hängt zwar nicht direkt von der Größe der Grundgesamtheit ab, jedoch ist eine indirekte Auswirkung vorhanden, da große Grundgesamtheiten in der Regel höhere Werte für die Anzahl enthalten.
Anzahl der Nachbarn ohne NULL-Rate
Im Feld "Number of Non-Null Neighbors" wird die Anzahl der Nachbarn, einschließlich des eigentlichen fokalen Features, aufgeführt, die keine NULL-Rate aufweisen. Features mit einem negativen oder NULL-Wert für den Parameter Feld mit Grundgesamtheit oder Zählfeld weisen eine NULL-Rate auf.Die Methoden mit räumlicher Glättung bestimmen die Rate eines Features anhand der Nachbarschaft des Features. Das Feld Number of Non-Null Neighbors gibt die Anzahl der Nachbarn an, die zum Glätten der Rate des fokalen Features verwendet wurden. Dieses Feld ist in der Ausgabetabelle oder -Feature-Class enthalten, wenn der Parameter Ratenmethode den Wert Lokal gewichtete Durchschnittsrate, Lokal gewichtete Medianrate oder Lokale empirische Bayes-Rate aufweist.
Fehlende Werte ausfüllen
Fill Missing Value ist ein boolesches Feld, das angibt, ob eine Rate für das Feature angerechnet wurde. Features mit einem negativen oder NULL-Wert für den Parameter Zählfeld oder Feld mit Grundgesamtheit weisen eine NULL-Rate auf. Wenn jedoch Ratenmethode den Wert Lokal gewichtete Durchschnittsrate oder Lokal gewichtete Medianrate aufweist, kann für ein Feature mit einer NULL-Rate eine Rate angerechnet werden. Wenn das Feature Nachbarn ohne NULL-Rate aufweist, wird die NULL-Rate durch den Schätzwert der lokal gewichteten Durchschnittsrate oder der lokal gewichteten Medianrate seiner Nachbarschaft ersetzt.
Gruppen-Layer und Gruppensymbolisierung
Das Werkzeug fügt dem Bereich Inhalt einen Gruppen-Layer und einen Sublayer für jede Rate hinzu. Wenn mehr als 10 Raten berechnet werden, werden nur die ersten 10 Raten als Sublayer hinzugefügt.
Jeder Sublayer verfügt über eine Standardabweichungskarte. Die Raten werden entsprechend ihrer Standardabweichung in Abschnitte unterteilt. Jeder Abschnitt wird mit dem Standardabweichungsintervall und dem entsprechenden Ratenintervall (in Klammern) beschriftet. Der Farbverlauf umfasst drei Farben: Grün, Weiß in der Mitte und Braun. Der Farbverlauf ist um die mittlere Rate zentriert. Die Raten von Features mit grüner Schattierung sind niedriger als die mittlere Rate. Die Raten von Features mit brauner Schattierung sind höher als die mittlere Rate. Features mit der stärksten Braunschattierung (+3 Standardabweichungen) und mit der stärksten Grünschattierung (-3 Standardabweichungen) sind Ausreißer.
Geoverarbeitungsmeldungen
Die Geoverarbeitungsmeldungen bieten eine Zusammenfassung der Features und Raten. Die Meldungen enthalten einen Dropdown-Abschnitt für jede berechnete Rate. Jeder Abschnitt enthält die Tabelle Zusammenfassung von Raten. Wenn der Parameter Ratenmethode den Wert Lokal gewichtete Durchschnittsrate, Lokal gewichtete Medianrate oder Lokale empirische Bayes-Rate aufweist, enthält jeder Abschnitt außerdem die Tabelle "Zusammenfassung der Nachbarschafts-Anzahlwerte".
Zusammenfassung von Raten
Wenn der Wert des Parameters Ratenmethode nicht Bruttorate lautet, enthält die Tabelle "Zusammenfassung von Raten" eine Spalte mit der ausgewählten Ratenmethode und eine weitere Spalte, in der die Bruttoraten zusammengefasst werden. Anhand dieser Spalten können Sie die Ergebnisse der ausgewählten Ratenmethode mit den Ergebnissen der Methode "Bruttorate" vergleichen. Die Tabelle "Zusammenfassung von Raten" enthält die Werte Minimum, Maximum, Medianwert, Mittelwert und die Standardabweichung der Raten. Wenn der Parameter Ratenmethode den Wert Lokal gewichtete Durchschnittsrate oder Lokal gewichtete Medianrate aufweist, enthält die Tabelle die Zeilen Features mit NULL-Raten-Wert und Features mit ausgefüllten Werten. In der Zeile Features mit NULL-Raten-Werten wird die Anzahl der Features aufgeführt, deren Rate NULL ist. In der Zeile Features mit ausgefüllten Werten wird die Anzahl der Features aufgeführt, die eine angerechnete Rate aufweisen. Diese Features hatten ursprünglich eine NULL-Rate. Ihre Nachbarschaft enthielt jedoch Ratenwerte ungleich NULL, und deren Rate wurde angerechnet.
Zusammenfassung der Nachbarschafts-Anzahlwerte
Wenn der Parameter Ratenmethode den Wert Lokal gewichtete Durchschnittsrate, Lokal gewichtete Medianrate oder Lokale empirische Bayes-Rate aufweist, enthält jeder Abschnitt außerdem die Tabelle "Zusammenfassung der Nachbarschafts-Anzahlwerte", in der alle Nachbarschaften zusammengefasst werden. Die Tabelle enthält das Minimum, das Maximum, den Medianwert und den Mittelwert der Nachbarschaftsanzahl sowie den numerischen Wert Features ohne Nachbarn.
Zusätzliche Quellen
Siehe die folgenden zusätzlichen Ressourcen:
- Anselin, L.; N. Lozano und J. Koschinsky. 2006."Rate Transformations and Smoothing"
- Brillinger, D. R. 1986. "A biometrics invited paper with discussion: the natural variability of vital rates and associated statistics." Biometrics, 693–734. https://pubmed.ncbi.nlm.nih.gov/3814721/
- Carlin, B.P. und Louis, T.A. 1997. "Bayes and empirical Bayes methods for data analysis." Statistics and Computing, 153–154. https://doi.org/10.1023/A:1018577817064
- Marshall, R.J. 1991. "Mapping disease and mortality rates using empirical Bayes estimators." Journal of the Royal Society Series C: (Applied Statistics), 283–294. https://doi.org/10.2307/2347593
- Martuzzi, M. und Elliott, P. 1996. "Empirical Bayes estimation of small prevalence of non-rare conditions." Statistics in Medicine, 15(17-18), 1867–1873. https://doi.org/10.1002/(SICI)1097-0258(19960915)15:17<1867::AID-SIM398>3.0.CO;2-2
- National Center for Health Statistics. 2019. Technical appendix from vital statistics of United States 1999 mortality
- Ulm, K. 1990. "Simple method to calculate the confidence interval of a standardized mortality ratio (SMR)." American Journal of Epidemiology, 131(2), 373–375. https://doi.org/10.1093/oxfordjournals.aje.a11507