Ajuster la distance rencontrée à l'aide d'un facteur vertical

Disponible avec une licence Spatial Analyst.

Une fois que la distance en ligne droite a été calculée, vous pouvez utiliser le facteur vertical pour contrôler la fréquence de rencontre de la distance. Vous pouvez également utiliser la surface de coût, les caractéristiques du sujet et le facteur horizontal pour contrôler la fréquence.

Le facteur vertical prend en compte l'effort nécessaire pour se déplacer sur les pentes du paysage. Cet effort affecte le mode de rencontre de la distance. Monter peut demander plus d'effort, descendre, moins d'effort et traverser des pentes, un effort intermédiaire. Modifier la distance en ligne droite ajustée pour tenir compte de cet effort permet de capturer la fréquence de rencontre de la distance par le voyageur.

La descente nécessitant moins d'énergie, le voyageur peut couvrir plus rapidement la distance

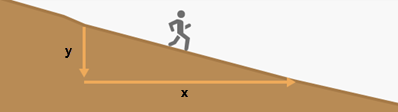
Ne confondez pas le facteur vertical, qui représente l'effort requis par les pentes, avec la distance de surface, qui représente un ajustement de la distance en ligne droite pour la distance réelle couverte par le voyageur lorsqu'il monte ou descend dans le paysage.

La pente est souvent pertinente pour l'analyse de la distance de coût. Intuitivement, il est plus coûteux de franchir des pentes plus raides que moins raides. En général, l'outil Spatial Analyst Pente permet de générer un raster de pente. Toutefois, il peut arriver que ce raster de pente ne soit pas correctement entré dans la surface de coût.

L'outil Pente calcule la descente la plus raide pour chaque cellule par rapport à ses huit voisins. Toutefois, comme nous l'avons précisé ci-avant, il est important de connaître le mode de rencontre de la pente lors du déplacement dans une cellule. Le voyageur peut éviter une cellule à laquelle une pente raide a été affectée dans une surface de coût. Cela peut s'avérer efficace si le voyageur remonte cette pente lorsqu'il se déplace dans la cellule. Toutefois, si le voyageur descend cette pente ou la traverse lorsqu'il se déplace dans la cellule, cette cellule peut être préférable pour le déplacement.

Vous pouvez prendre en compte l'effort de franchissement de la pente à l'aide du raster d'altitude dans le facteur vertical. N'incluez pas le raster de pente dans la surface de coût si le sens de rencontre de la pente est important.

Le sens de calcul des pentes dans le facteur vertical peut également être modifié par le paramètre Sens de déplacement des caractéristiques de la source. En effet, se déplacer vers ou depuis une source change le sens dans lequel le voyageur pénètre dans une cellule et donc le mode de rencontre de la pente.

L'incorporation du facteur vertical (VF) est un modificateur multiplicateur des calculs de distance en ligne droite ajustée. Des détails sur le mode de calcul du facteur vertical sont fournis dans la rubrique Algorithme d'accumulation de distance.

Exemples d'utilisation du facteur vertical

Le facteur vertical peut être utilisé dans divers scénarios, tels que les suivants :

• Rechercher un nouveau chemin de randonnée entre deux campements qui n'est pas plus long, mais plus facile à parcourir que randonner directement le long de l'itinéraire le plus court.
• Examiner l'impact du salage des routes en hiver sur la santé de la végétation environnante. La végétation en aval de la route sera plus affectée par le ruissellement.
• Déterminer les déplacements d'une créature marine qui dépendent du changement de concentration en sel.

Incorporer un facteur vertical

L’analyse de distance peut se diviser de manière conceptuelle entre les domaines fonctionnels associés suivants :

• Calculer la distance en ligne droite et, éventuellement, ajuster les calculs avec un raster d’interruption ou un raster de surface.
• Une fois que la distance en ligne droite a été calculée, déterminez éventuellement la fréquence de rencontre de la distance via une surface de coût, les caractéristiques de la source, un facteur vertical et un facteur horizontal. Créez le raster de distance cumulée.
• Connecter les régions sur la surface de distance cumulée résultante à l’aide d’un réseau optimal, de chemins spécifiques ou d’un couloir.

À partir de la deuxième zone fonctionnelle, déterminez la fréquence de rencontre de la distance via un facteur vertical, comme illustré ci-après. Ce scénario implique une collection de quatre postes de garde forestier (points violets) et des rivières (lignes bleues).

La distance de plus faible coût entre chaque cellule et les postes de garde forestier les plus proches incorpore une interruption, un raster de surface et une surface de coût.

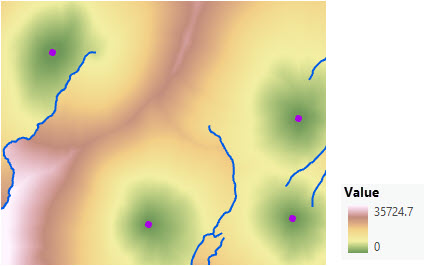
Pour incorporer l'effort que doivent fournir les gardes forestiers pour franchir les pentes, un facteur vertical est spécifié. La surface d'altitude est utilisée comme raster vertical.

Distance de plus faible coût entre chaque cellule et le poste de garde forestier le plus proche, qui incorpore le facteur vertical dans la carte ci-avant qui inclut une interruption, un raster de surface et une surface de coût. Le facteur vertical influence le centre de la zone d'étude en particulier.

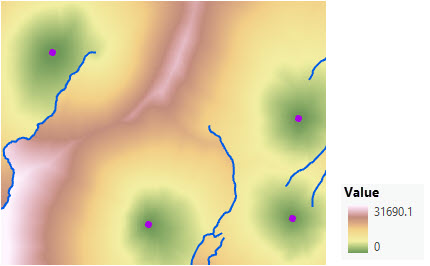
Créer un raster de distance à l'aide d'un facteur vertical

Pour créer une carte de distance qui incorpore un facteur vertical, procédez comme suit :

1. Ouvrez l'outil Accumulation de distance.
2. Spécifiez une source pour le paramètre Données raster ou vecteur source en entrée.
3. Nommez le raster d’accumulation de distance en sortie.
4. Développez la catégorie Coûts relatifs au mouvement vertical.
5. Spécifiez un raster de facteur vertical pour le paramètre Raster vertical en entrée.

   Cette entrée est utilisée pour calculer la pente rencontrée lors du déplacement entre les cellules. En général, un raster d'altitude doit être spécifié.

   Le paramètre Facteur vertical apparaît.

6. Spécifiez les valeurs du paramètre Facteur vertical.

   Ce paramètre identifie le multiplicateur à appliquer au coût pour tenir compte de l'effort nécessaire pour se déplacer sur les pentes rencontrées.

7. Cliquez sur Exécuter.

Le facteur vertical a un impact sur la fréquence de rencontre de la distance.

Pour modifier la fréquence de rencontre de la distance et tenir compte de l'effort à fournir par le voyageur pour franchir les pentes, l'outil effectue deux actions en interne :

• Il calcule le mode de rencontre de la pente lors du déplacement d'une cellule à la suivante. Cela s'appelle l'angle de déplacement relatif vertical (VRMA).
• Il identifie la manière dont l'angle VRMA modifie la fréquence de rencontre de la distance.

Calculer l'angle VRMA

L'angle VRMA correspond à l'angle de la pente entre la cellule de traitement (cellule source) et la cellule vers laquelle le voyageur se dirige (cellule de destination). La distance est calculée pour la cellule de destination. Les hauteurs à partir desquelles les pentes sont calculées sont définies par le raster de facteur vertical en entrée.

Cette pente est calculée à l'aide du théorème de Pythagore avec la formule hauteur/distance parcourue. La base du triangle permettant de déterminer la pente est dérivée de la distance en ligne droite ajustée. La hauteur est établie en soustrayant la cellule source de la cellule de destination. L'angle qui en résulte s'appelle l'angle VRMA.

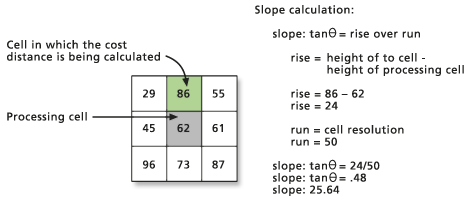
Le VRMA est exprimé en degrés. Les valeurs de l'angle VRMA sont comprises entre -90 et + 90 degrés, pour tenir compte à la fois des pentes positives et négatives.

Identifier le multiplicateur VF (facteur vertical)

Vous pouvez ensuite tracer la valeur VRMA sur le graphique du facteur vertical spécifié pour obtenir le multiplicateur de facteur vertical à utiliser dans les calculs qui déterminent le coût d'accès à la cellule de destination. La distance de déplacement dans la cellule est multipliée par le facteur vertical identifié. Plus le facteur est important, plus le mouvement est difficile. Un facteur vertical supérieur à 1 augmente la distance de coût rencontrée. Un facteur vertical strictement compris entre 0 et 1 permet au voyageur de rencontrer plus rapidement les distances.

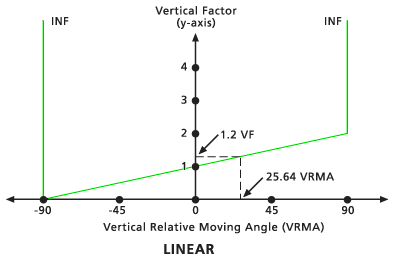
Par exemple, le diagramme suivant montre la relation entre le facteur vertical et l'angle VRMA dans une fonction de facteur vertical linéaire :

La relation entre le facteur vertical et l'angle VRMA est illustrée dans un diagramme linéaire.

Les fonctions de facteur vertical vous permettant de capturer l'interaction du voyageur avec les pentes qu'il rencontre sont les suivantes : Binaire, Linéaire, Linéaire inverse, Linéaire symétrique, Linéaire inverse symétrique, Cos, Sec, Cos-Sec et Sec-Cos. Pour des informations détaillées sur chaque fonction, consultez la section Informations supplémentaires ci-après.

Remarque :

Le facteur vertical est un multiplicateur. Soyez prudent lorsque vous spécifiez les unités lors de la combinaison du facteur vertical à une surface de coût, aux caractéristiques de la source ou à un facteur horizontal. En général, lors de la saisie d'une surface de coût, le facteur vertical doit correspondre à un ajustement par multiplicateur de la fréquence des unités de surface de coût. Si le temps est l'unité de la surface de coût, le facteur vertical doit être un modificateur du temps. Un seul de ces facteurs peut définir les unités de la fréquence. Les autres facteurs ne possèdent pas d'unité et leurs valeurs sont des modificateurs multiplicateurs des unités spécifiées.

Exemples d'applications qui utilisent un facteur vertical

Des exemples d'applications qui utilisent un facteur vertical sont décrits ci-dessous.

Créer une zone tampon de pente descendante pour comprendre l'impact du salage hivernal sur la végétation

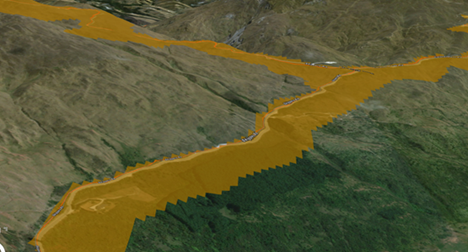
Vous souhaitez identifier les zones en pente descendante à 50 mètres d'une route car ces zones peuvent être affectées par le ruissellement de l'eau salée en hiver. Vous souhaitez mesurer la distance le long de la surface du terrain. Vous pouvez utiliser le paramètre de facteur vertical Binaire pour empêcher l'outil Accumulation de distance d'identifier les cellules en amont des cellules de route. Des exemples de zones tampon de pente descendante résultantes sont illustrés ci-après.

Les zones pouvant être affectées par le ruissellement du salage hivernal sous les routes sont identifiées. À l'aide de l'accumulation de distance et du paramètre de facteur vertical binaire, il est possible de déterminer les cellules de pente descendante dont la distance de surface est inférieure ou égale à 50 mètres des routes (ombrage orange).

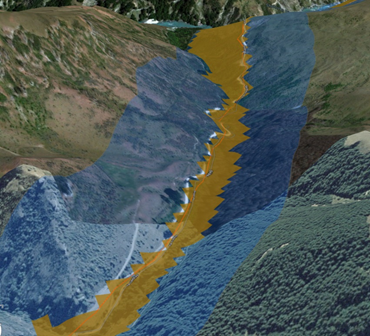
À titre de comparaison, une autre section de la route montrant la différence entre les zones tampon de ligne droite et de pente descendante seule est illustrée ci-après.

Zone tampon de distance en ligne droite de 50 mètres (ombrage bleu) superposée à une zone tampon de distance de surface de pente descendante seule (ombrage orange). Cette dernière est plus étroite aux localisations où vous ne pouvez pas descendre sur 50 mètres.

Pour créer une zone tampon de pente descendante, procédez comme suit :

1. Ouvrez l'outil Accumulation de distance.
2. Entrez les routes dans le paramètre Données raster ou vecteur source en entrée.
3. Nommez la valeur Raster d’accumulation de distance en sortie.
4. Développez la catégorie Coûts relatifs au mouvement vertical.
5. Fournissez un raster d'altitude dans le paramètre Raster vertical en entrée.
6. Spécifiez Binaire pour le paramètre Facteur vertical.
7. Développez la catégorie Caractéristiques de la source.
8. Définissez le paramètre de distance Accumulation maximale sur 50 mètres.
9. Cliquez sur Exécuter.

Fonction de randonnée de Tobler

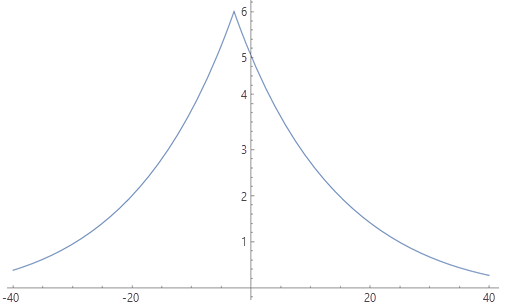
Vous souhaitez calculer le temps de randonnée dans le paysage, tout en ajustant la vitesse de marche en fonction de la pente rencontrée dans le sens de déplacement. La fonction de randonnée de Tobler (1993) est un modèle empirique permettant d'effectuer cet ajustement. Ce modèle utilise une vitesse de marche de base de 6 km/h, qui correspond à un déplacement sur une pente légèrement descendante (environ trois degrés).

La fonction S est définie en fonction de la pente d (en degrés), selon la formule suivante : S = tan(d π/180)

La fonction de vitesse W se présente comme suit :

Fonction de vitesse de Tobler comme fonction de la pente en degrés exprimée en km/h. La vitesse de déplacement maximale de 6 km/h est atteinte lors d'une marche sur un terrain légèrement descendant.

Vous souhaitez connaître le temps nécessaire pour parcourir une distance donnée (une cellule) et non la distance que vous pouvez parcourir en un temps donné. Vous devez donc utiliser la réciproque de la vitesse, à savoir, l'allure. L'allure est exprimée en heures par mètre et non en heures par kilomètre (car l'unité d'analyse de la distance horizontale est le mètre).

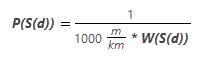
La fonction d'allure se présente comme suit :

Réciproque de la fonction de vitesse de Tobler, exprimée ici en heures par mètre, représentée comme fonction de pente en degrés.

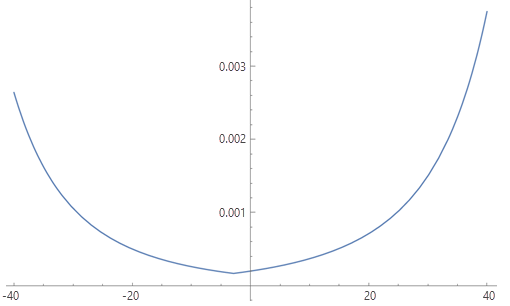
Déterminez la fonction P(S) d'une plage de valeurs de d et enregistrez-les dans un tableau (illustré dans la section Tableau ci-après). Ce tableau peut ensuite être utilisé avec la fonction de facteur vertical Tableau pour fournir un coût par cellule qui tient compte du sens de déplacement dans une cellule. Le coût (en temps) du déplacement dans une cellule suivant un sens spécifique et de la rencontre d'une pente d est P(S(d)) * taille de cellule (en mètres).

Pour utiliser une surface de friction de coût en entrée non directionnelle en plus de la fonction de randonnée (allure) de Tobler dans la même analyse, prêtez attention aux unités de l'entrée de friction de coût. Pour chaque cellule, l'outil Accumulation de distance calculant P(S) * (coût d'entrée au niveau de la cellule), les valeurs ne peuvent pas utiliser toutes deux des unités d'allure. Vous pouvez modifier la fonction d'allure de Tobler pour qu'elle ne soit qu'une pondération (remplacez le 6 par un 1 si vous pensez que cela est justifié de manière empirique) ou utilisez des pondérations sans unité dans votre entrée de coût.

Informations supplémentaires

Les sections ci-après fournissent des informations supplémentaires sur les facteurs verticaux.

Facteurs verticaux

Pour définir une fonction de facteur vertical, vous pouvez en choisir une dans une liste de graphiques fournie ou créer une fonction personnalisée à l'aide d'un fichier ASCII. Les fonctions de facteur vertical suivantes sont disponibles dans l'outil Accumulation de distance :

Options, modificateurs et valeurs par défaut des facteurs verticaux

Fonction	Facteur zéro	Angle d'inflexion inférieur	Angle d'inflexion supérieur	Pente	Puissance	Puissance cos	Puissance sec
Binaire	1	-30	30	N/D	N/D	N/D	N/D
Linéaire	1	-90	90	1.111E-02	N/D	N/D	N/D
Linéaire inverse	1	-45	45	-2.222E-02	N/D	N/D	N/D
Linéaire symétrique	1	-90	90	1.111E-02	N/D	N/D	N/D
Linéaire inverse symétrique	1	-45	45	-2.222E-02	N/D	N/D	N/D
Cos	N/D	-90	90	N/D	1	N/D	N/D
Sec	N/D	-90	90	N/D	1	N/D	N/D
Cos – Sec	N/D	-90	90	N/D	N/D	1	1
Sec – Cos	N/D	-90	90	N/D	N/D	1	1

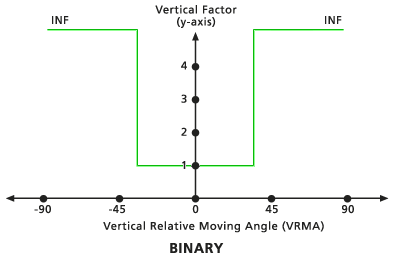
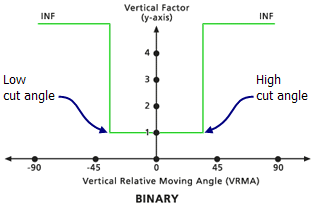
Binaire

Lorsqu'un VRMA est supérieur à l'angle de découpe inférieur et inférieur à l'angle de découpe supérieur, le FV permettant de déplacer les deux cellules a pour valeur celle qui est associée au facteur zéro. Si le VRMA est supérieur à l'angle de découpe, la valeur du FV est l'infini. L'angle de découpe par défaut est de 30 degrés si vous ne précisez rien.

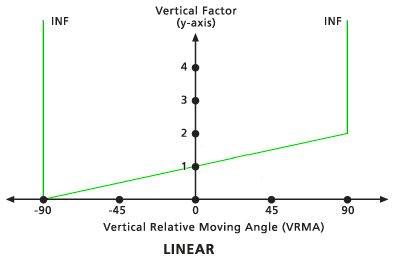
Linéaire

Les FH sont désignés par une ligne droite dans le système de coordonnées VRMA-FV. La ligne intercepte l'axe des y (équivalent du VF) à la valeur du facteur zéro. Vous pouvez définir la pente d'une ligne à l'aide du modificateur Pente. Si vous n'indiquez pas la pente, la valeur par défaut est 1/90 (désignée par 0,01111). L'angle de découpe inférieur par défaut est de -90 degrés. L'angle de découpe supérieur par défaut est de 90 degrés.

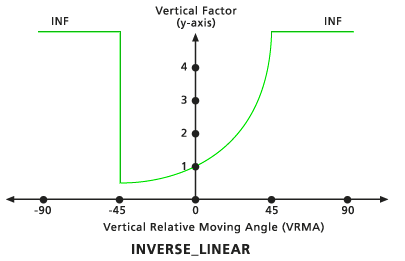
Linéaire inverse

Les FH sont régis par les valeurs inverses d'une ligne droite dans le système de coordonnées VRMA-FV. La ligne intercepte l'axe des y (équivalent du VF) à la valeur du facteur zéro. Vous pouvez identifier la pente d'une ligne avec le modificateur Pente. Si vous n'indiquez pas la pente, la valeur par défaut est -1/45 (désignée par 0,02222). L'angle de découpe inférieur par défaut est de -45 degrés. L'angle de découpe supérieur par défaut est de 45.

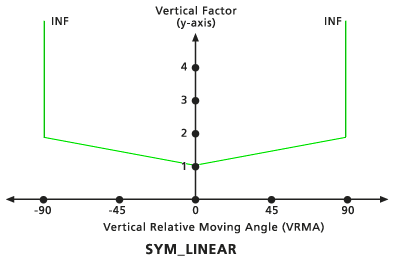
Linéaire symétrique

Ce facteur vertical est composé de deux fonctions linéaires relatives aux angles VRMA qui sont symétriques à l'axe VF (y). Les deux lignes interceptent à la fois l'axe des y à la valeur VF associée au facteur zéro. La pente des lignes est définie en tant que pente distincte relative au VRMA positif, à l'aide du modificateur du facteur vertical Pente, qui réplique les VRMA négatifs. La pente par défaut est de 1/90 (spécifié comme 0,01111). L'angle de découpe inférieur par défaut est de -90 et l'angle de découpe supérieur par défaut est de 90.

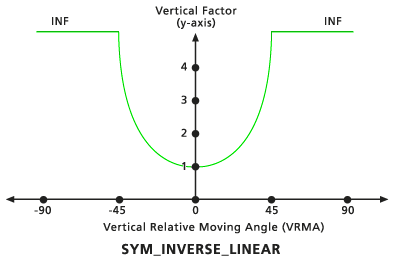
Linéaire inverse symétrique

Ce facteur vertical est l'inverse du mot-clé du facteur vertical Linéaire symétrique. Il se compose de deux fonctions linéaires inverses relatives aux angles VRMA, qui sont symétriques par rapport à l'axe VF (y). Les deux lignes interceptent l'axe des y à la valeur VF de 1. La pente des lignes est définie en tant que pente distincte relative au VRMA positif, à l'aide du modificateur du facteur vertical Pente, qui réplique les VRMA négatifs. La pente par défaut est de -1/45 (spécifié comme 0,02222). L'angle de découpe inférieur par défaut est de -45 et l'angle de découpe supérieur par défaut est de 45.

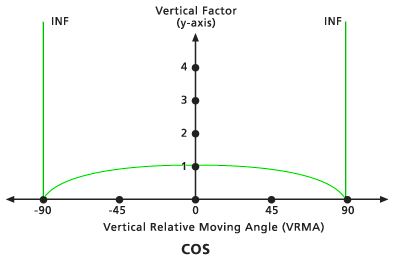
Cos

Le FV est régi par la fonction cosinus du VRMA. L'angle de découpe inférieur par défaut est de -90 degrés. L'angle de découpe supérieur par défaut est de 90 degrés. La valeur Puissance cos par défaut est de 1.0.

Sec

Le FV est régi par la fonction sécante du VRMA. L'angle de découpe inférieur par défaut est de -90 degrés. L'angle de découpe supérieur par défaut est de 90 degrés. La valeur Puissance sec par défaut est de 1.0.

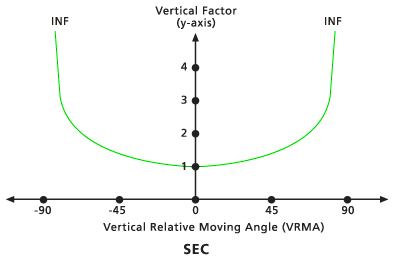
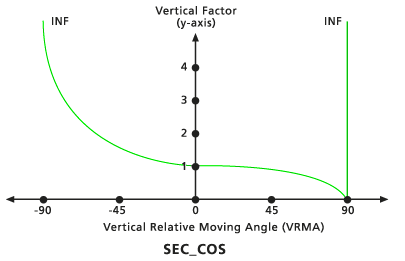
Cos - Sec

Lorsque le VRMA est une valeur de degré négative, le FV est défini par la fonction cosinus du VRMA. Si le VRMA est une valeur de degré positive, le FV est défini par la fonction sécante du VRMA. L'angle de découpe inférieur par défaut est de -90 degrés. L'angle de découpe supérieur par défaut est de 90 degrés. Les valeurs Puissance cos et Puissance sec par défaut sont toutes deux de 1.0.

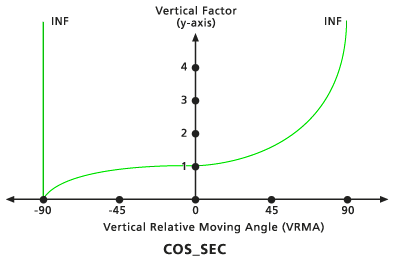
Sec - Cos

Lorsque le VRMA est une valeur de degré négative, le FV est défini par la fonction sécante du VRMA. Si le VRMA est une valeur de degré positive, le FV est défini par la fonction cosinus du VRMA. L'angle de découpe inférieur par défaut est de -90 degrés. L'angle de découpe supérieur par défaut est de 90 degrés. Les valeurs Puissance sec et Puissance cos par défaut sont toutes deux de 1.0.

Table

Une table est un fichier ASCII comprenant deux colonnes sur chaque ligne.

La première colonne identifie l'angle VRMA en degrés et la seconde, le facteur vertical (VF). Chaque ligne précise un point. Deux points consécutifs produisent un segment de ligne dans le système de coordonnées VRMA-VF. Les angles doivent être saisis par ordre croissant et vont de -90 à 90. Le facteur FV de tous les angles VRMA inférieurs (le plus faible) à la première valeur en entrée ou supérieurs à la dernière valeur en entrée (la plus élevée) correspond à l'infini. Un FV infini est représenté par -1 dans la table ASCII.

Vous trouverez ci-après un exemple de table ASCII de facteur vertical. Les unités de la première colonne sont les degrés et celles de la deuxième colonne, les heures par mètre.

    -90  -1
    -80  -1
    -70   2.099409721
    -60   0.060064462
    -50   0.009064613
    -40   0.00263818
    -30   0.001055449
    -20   0.000500142
    -10   0.00025934
      0   0.000198541
     10   0.000368021
     20   0.000709735
     30   0.001497754
     40   0.003743755
     50   0.012863298
     60   0.085235529
     70   2.979204206
     80  -1
     90  -1

Modificateurs du facteur vertical

Vous pouvez contrôler davantage la fonction VRMA à l'aide de modificateurs qui permettent d'affiner les facteurs verticaux. Il peut exister un angle seuil tel que si l'angle HRMA le dépasse, le coût devient si important qu'il empêche le déplacement. Ce seuil s'appelle l'angle de découpe. Le FV est attribué à l'infini lorsque le VRMA dépasse cette valeur.

Le diagramme d'un facteur vertical affiche à la fois les angles de découpe inférieur et supérieur, tandis que le diagramme d'un facteur horizontal n'affiche qu'un seul angle de découpe.

À l'aide de ces modificateurs, vous pouvez attribuer des angles de découpe à chaque fonction, élever des courbes trigonométriques à une puissance, employer le facteur zéro pour modifier l'interception des fonctions non trigonométriques sur l'axe des y et définir la pente d'une ligne dans les fonctions linéaires.

Facteur zéro

Ce modificateur établit le facteur vertical utilisé lorsque l'angle VRMA est nul. Ce facteur positionne l'interception avec l'axe des y de la fonction spécifiée.

Angle d'inflexion inférieur

Ce modificateur représente l'angle VRMA en degrés qui définit le seuil inférieur au-dessous duquel les facteurs verticaux (VF) sont définis sur l'infini, quels que soient les mots clés du facteur vertical indiqués.

Angle d'inflexion supérieur

Ce modificateur représente l'angle VRMA en degrés qui définit le seuil supérieur au-dessus duquel les facteurs verticaux (VF) sont définis sur l'infini, quels que soient les mots clés du facteur vertical indiqués.

Pente

Ce modificateur Identifie la pente des lignes droites dans le système de coordonnées VRMA-VF pour les mots-clés Linéaire, Linéaire inverse, Linéaire symétrique et Linéaire inverse symétrique. La pente est désignée comme étant la hauteur sur la distance parcourue (par exemple, une pente de 30 degrés correspond à 1/30, soit 0,03333). Pour obtenir un exemple de fonction linéaire avec une pente de 1/90, reportez-vous au diagramme VRMA linéaire.

Puissance

Ce modificateur représente la puissance à laquelle les valeurs sont élevées.

Puissance cos

Ce modificateur représente la puissance à laquelle les valeurs non négatives de la fonction VRMA Sec-Cos et les valeurs négatives de la fonction VRMA Cos-Sec sont élevées. Le FV est régi par les éléments suivants :

VF = cos(VRMA)power

Puissance sec

Ce modificateur représente la puissance à laquelle les valeurs non négatives de la fonction VRMA Cos-Sec et les valeurs négatives de la fonction VRMA Sec-Cos sont élevées. Le FV est régi par les éléments suivants :

VF = sec(VRMA)power

Nom de la table

Ce modificateur identifie le nom du fichier ASCII à utiliser avec le mot-clé du facteur vertical Table.

Bibliographie

Tobler, Waldo (1993) Three Presentations on Geographical Analysis and Modeling: Non-Isotropic Geographic Modeling; Speculations on the Geometry of Geography; and Global Spatial Analysis (93-1) Retrieved from https://escholarship.org/uc/item/05r820mz