Disponible avec une licence Spatial Analyst.
L'outil Connectivité de coût se concentre sur la définition du réseau optimal de chemins de moindre coût et non sur la création de chemins séparés reliant une région à une autre. Dans le réseau généré, les phénomènes peuvent passer d'une région à une autre à l'aide des chemins (ils peuvent dans ce cas traverser d'autres régions).
Exemple de problèmes résolus par l'outil Connectivité de coût
- Dans un modèle d'aptitude, vous avez identifié 10 des meilleures parcelles d'habitat pour les lynx. Vous voulez que les lynx se déplacent d'une parcelle à une autre via le réseau le plus efficace possible de couloirs de circulation pour la faune sauvage afin de préserver la diversité génétique au sein de la métapopulation.
- Dans un déploiement militaire de maintien de la paix, vous avez identifié 5 zones dans lesquelles positionner les troupes et le personnel. Vous voulez développer le meilleur réseau possible d'itinéraires de ravitaillement entre les différentes bases.
- Dans une exploitation forestière, vous voulez créer le réseau le plus efficace possible, en termes de coût, de chemins forestiers pour en extraire du bois.
Fonctionnement de l'algorithme de connectivité de coût
Les étapes suivantes expliquent le fonctionnement conceptuel de l'algorithme Connectivité de coût :
- Les surfaces de coût et les sources en entrée sont identifiées.
Dans le graphique ci-dessous, les régions en entrée (polygones colorés) apparaissent au-dessus de la couche de surface de coût.
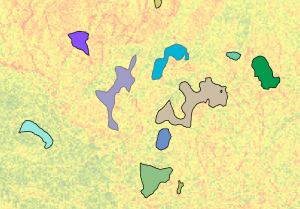
Les régions en entrée apparaissent sur le raster de surface de coût. - Une Allocation de coût est effectuée.
Dans le graphique ci-dessous, les régions en entrée apparaissent sur la couche d'allocation de coût associée. La valeur de chaque cellule du raster d'allocation correspond à celle d'une région spécifique accessible au coût cumulé le plus faible.
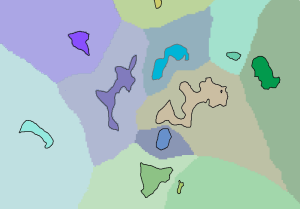
Régions affichées sur la couche d'allocation de coût - Des chemins de coût sont créés entre chaque région et sa région de coût voisine.
Dans le graphique ci-dessous, les régions en entrée et les chemins de moindre coût de chaque région vers sa région de coût voisine (lignes magenta) sont affichées sur la couche d'allocation de coût associée.
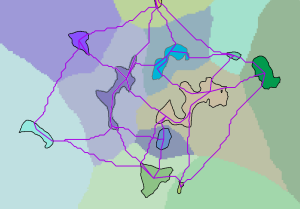
Allocation de coût avec des régions connectées par des chemins - Les régions et les chemins résultants sont convertis en un diagramme (dans la théorie des graphes). Dans la conversion, les régions sont les sommets et les chemins les tronçons. Le coût cumulé du chemin est le poids du tronçon.
En théorie, la conversion des régions et des chemins en théorie des graphes peut être représentée par l'illustration suivante. Les cercles numérotés sont les sommets (les régions) et les lignes de connexion entre les sommets sont les tronçons (les chemins de moindre coût). Les poids des tronçons représentent le coût cumulé des chemins. Sur l'illustration, plus le coût est élevé, plus la ligne est épaisse.
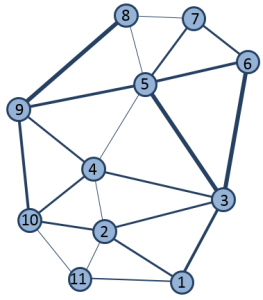
Illustration conceptuelle de la théorie des graphes Remarque :
Pour bien comprendre le fonctionnement de cet outil, nous vous conseillons de vous familiariser avec la théorie des graphes. De nombreuses ressources sont disponibles, mais vous pouvez dans un premier temps consulter l'entrée Wikipedia sur https://en.wikipedia.org/wiki/Graph_theory.
- L'arbre couvrant de poids minimal est déterminé via la théorie des graphes pour connecter les sommets (les régions) de la manière la plus efficace possible (moindre coût).
Remarque :
Vous trouverez plus d'informations sur les arbres couvrants de poids minimal sur Internet, et notamment dans l'entrée Wikipedia sur https://en.wikipedia.org/wiki/Minimum_spanning_tree.
- La représentation spatiale des régions et des chemins à partir des arbres couvrants de poids minimal est appariée à une classe d'entités en sortie.
Dans le graphique ci-dessous, les régions en entrée et le réseau de chemins de moindre coût des arbres couvrants de poids minimal (couleur magenta) apparaissent sur la couche de surface de coût associée.
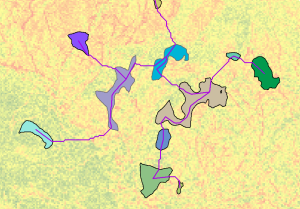
Chemins en sortie entre les régions apparaissant sur le raster de coût - Une classe d'entités des chemins vers les régions de coût voisines peut également être produite en sortie (voir l'étape 3 ci-dessus).
Chaque chemin représentera une entité linéaire distincte et on remarquera des lignes en double là où les couloirs suivent un segment commun.
Si les régions en entrée sont des polygones, les chemins sont prolongés jusqu'à un point dans le polygone pour permettre au voyageur d'entrer par un chemin, de se déplacer dans la région et de sortir par un autre chemin, pour atteindre une région éloignée. Aucun coût n'est imputé à ces segments prolongés dans une région. Ainsi, aucun coût n'est associé aux déplacements dans la région. C'est également le cas pour les régions linéaires. Aucun coût n'est associé aux déplacements le long de l'entité linéaire pour rejoindre un autre chemin.
Dans le graphique ci-dessous, le côté gauche est généré par l'application des outils Distance de coût et Chemin de coût qui permettent de connecter des régions. Vous remarquerez que les chemins n'atteignent que le tronçon des régions. L'image à droite affiche le réseau résultant de chemins connectant les régions via l'outil Connectivité de coût. Vous remarquerez que les chemins se poursuivent dans la région pour permettre au voyageur d'y pénétrer par un chemin et de la quitter par un autre chemin.
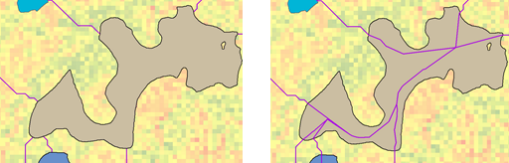
Importance des régions
Dans l'outil Connectivité de coût, les données en entrée doivent être des régions. Une région est une série connectée de cellules (adjacentes) de valeur identique. Les cellules déconnectées de valeur identique sont appelées des zones. Vous pouvez convertir des zones en régions à l'aide de l'outil Groupes par régions. L'outil Connectivité de coût permet de connecter les régions les unes aux autres pour que toutes les régions et les cellules qu'elles contiennent soient accessibles via le réseau obtenu.
Scénarios de workflow de connectivité de coût
Voici les scénarios les plus courants d'utilisation de l'outil Connectivité de coût.
- La sortie souhaitée est le réseau optimal (l'arbre couvrant de poids minimal).
- Ajoutez des chemins spécifiques au réseau optimal via les outils Distance de coût et Chemin de coût pour connecter des régions que le réseau optimal ne peut pas capturer. On peut citer, par exemple, l'ajout d'une voie d'évacuation qui permet aux pompiers d'échapper à un incendie.
- Créez le réseau souhaité à partir de la sortie facultative de tous les chemins vers les régions voisines en sollicitant l'avis d'experts pour supprimer les chemins superflus.
- Transformez l'un des scénarios ci-dessus en un réseau Network Analyst et effectuez une analyse supplémentaire des déplacements entre les régions.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?