Как работает инструмент Бивариантная пространственная связь (L-статистика Ли)

Инструмент Бивариантная пространственная связь (L-статистика Ли) измеряет пространственную связь (зависимость) между двумя непрерывными переменными анализа, вычисляя L-статистику Ли. Статистика характеризует степень корреляции переменных и схожесть их структур (сходство пространственной кластеризации). L-статистика Ли будет находиться в диапазоне от -1 до 1 и концептуально аналогично коэффициенту корреляции, но скорректировано с учетом пространственной автокорреляции двух переменных. Значения L Ли, близкие к 1, указывают на то, что переменные в высшей степени положительно коррелируют (когда одно значение высокое, другое, как правило, также высокое) и что каждая переменная имеет высокую пространственную автокорреляцию (высокие и низкие значения каждой из переменных имеют тенденцию к совместной кластеризации). Значения, близкие к -1, указывают на то, что переменные в высшей степени отрицательно коррелируют (когда одно значение высокое, другое, как правило, низкое) и что каждая переменная имеет высокую пространственную автокорреляцию. Значения, близкие к 0, указывают на то, что переменные пространственно не связаны, это означает, что они либо некоррелированы, либо что они не являются пространственно автокоррелированными. Статистика также может быть распределены локально по каждому входному объекту и распределена по категориям, чтобы вы могли исследовать, как меняется пространственная связь переменных анализа в исследуемой области.

Учет пространственной автокорреляции переменных важен для оценки пространственной связи между анализируемыми переменными, поскольку традиционные статистические тесты, основанные на корреляции Пирсона, недействительны, когда переменные пространственно автокоррелированы. Кроме того, эти традиционные тесты не оценивают схожесть двух переменных, что является критическим аспектом пространственной взаимосвязи между переменными.

L-статистика Ли рассчитывается путем объединения корреляции локальных средних соседств двух переменных анализа и корректировки корреляции с помощью скаляров пространственного сглаживания для каждой переменной анализа. Скаляры пространственного сглаживания - это значения между 0 и 1. Сглаживающие скаляры, близкие к 1, указывают на сильную пространственную автокорреляцию (положительную или отрицательную), а значения, близкие к 0, указывают на то, что значения являются пространственно случайными и не автокоррелированы. Малые скаляры пространственного сглаживания уменьшат L-статистику Ли относительно корреляции Пирсона, чтобы скорректировать отсутствие пространственной кластеризации переменных.

На следующих изображениях показаны различные примеры карт двух переменных анализа и связанных с ними корреляций Пирсона и L-статистики Ли для этих переменных. На каждом изображении синие треугольники имеют значение 1, а оранжевые треугольники - значение 0.

На первом рисунке ниже обе переменные анализа имеют одинаковые значения в каждом местоположении, поэтому их корреляция по Пирсону равна 1. Кроме того, каждый из них имеет высокую положительную пространственную автокорреляцию, при этом высокие и низкие значения группируются вместе. Это приводит к значению L-статистики Ли, равному 0,801, что указывает на высокую положительную пространственную связь между переменными.

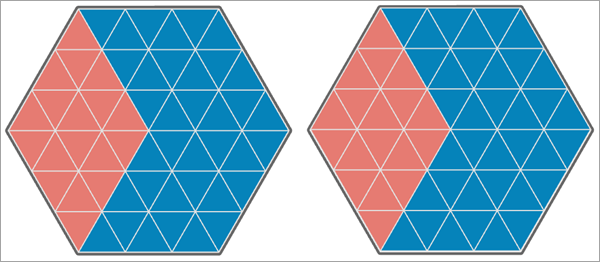
На втором изображении ниже значения второй переменной анализа сдвинуты на один треугольник вправо, так что 30 из 54 треугольников имеют совпадающие значения. Это дает корреляцию Пирсона, равную 0,167. Однако из-за сильной пространственной автокорреляции каждой переменной анализа, L-статистика Ли немного выше: 0,186. Это указывает на слабую или умеренную положительную пространственную связь между переменными.

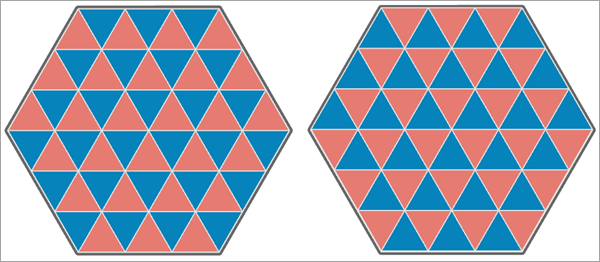
На третьем изображении ниже значения второй аналитической переменной сдвинуты на другую сторону гексагональной области изучения, и 18 из 54 треугольников имеют совпадающие значения. Это приводит к тому, что корреляция Пирсона равна -0,500, а L-статистика Ли равна -0,490, что указывает на от умеренной до сильной отрицательной пространственной связью между переменными.

На последнем рисунке ниже обе переменные анализа имеют отрицательную пространственную автокорреляцию, и ни один из треугольников не имеет одинакового значения. В результате корреляция Пирсона равна -1, а L-статистика Ли равна -0,204, что указывает на слабую или умеренную отрицательную пространственную связь между переменными.

Локальная L-статистика Ли

L-cтатистика Ли может быть распределена по каждому входному объекту, чтобы увидеть, как пространственная связь между переменными изменяется пространственно и локально. Некоторые регионы или местоположения могут иметь более высокую или более низкую пространственную связь, чем общая (глобальная) L-статистика Ли, из-за изменения локальных корреляций и локального пространственного сглаживания. Вы можете определить, является ли локальная пространственная связь выше или ниже глобальной пространственной связи, непосредственно сравнивая значения локальной L-статистики Ли с глобальной L-статистикой Ли. В отличие от глобальной статистики, локальная статистика может быть больше 1 или меньше -1, а среднее значение локальной статистики всегда равно глобальной статистике.

Вы также можете классифицировать локальную L-статистику Ли по нескольким категориям в зависимости от их статистической значимости и значений окрестностей каждого объекта. Существует пять возможных категорий для каждого объекта: Not Significant, High-High, High-Low, Low-High и Low-Low. Если локальная L-статистика Ли не является значимой для какого-либо объекта по крайней мере на 90 процентов, он будет классифицирован как Не значимый. В противном случае, если среднее значение окрестности первой переменной анализа больше среднего значения первой переменной анализа, а среднее значение окрестности второй переменной больше среднего значения второй переменной, оно будет классифицировано как High-High. Аналогично, если первая переменная меньше среднего значения, а вторая переменная больше среднего значения, она будет классифицирована как Low-High (и наоборот). Важно различать эти категории, потому что если две переменные положительно связаны в пространстве, это означает, что низкие значения и высокие значения двух переменных имеют тенденцию к объединению. Однако в обеих ситуациях результатом будет большая локальная L-статистика Ли, поэтому категории уточняют, имеет ли каждый объект высокую степень связи из-за того, что обе переменные высокие, или из-за того, что обе переменные низкие. Таким же образом, для отрицательной пространственной связи классификации показывают, имеет ли объект отрицательную локальную L-статистику Ли, потому что первая переменная высокая, а вторая переменная низкая, или же первая переменная низкая, а вторая переменная высокая.

При запуске на активной карте выходной слой объектов будет отображаться на основе этих пяти категорий. Для переменных с положительной пространственной связью (глобальная L-статистика Ли больше 0), слой будет содержать в основном категории High-High и Low-Low. Для переменных с отрицательной пространственной связью (глобальная L-статистика Ли меньше 0), слой будет содержать в основном категории High-Low и Low-High.

Пример случаев использования

Вы можете использовать этот инструмент в следующих сценариях:

• Исследуйте пространственную связь между уровнем образования и доходами домохозяйств в разных районах крупного города. Соответствуют ли области более высокого уровня образования областям с более высоким доходом домохозяйств?
• Исследуйте пространственную связь между растительным покровом и качеством воздуха. Улучшается ли качество воздуха в районах с большим количеством растительности? Является ли эта связь статистически значимой?
• Существует ли взаимосвязь между уровнем преступности и стоимостью недвижимости? Меняется ли отношение в разных районах мегаполиса?

Перестановки и p-значения

Вы можете проверить глобальную и локальную L-статистику Ли на предмет статистической значимости, используя перестановки. В результате перестановок все значения двух переменных анализа случайным образом переназначаются в новое местоположение (сохраняя два значения в паре в каждом новом местоположении), и для перестановочных значений вычисляется глобальная и локальная L-статистика Ли. Этот процесс повторяется большое количество раз (в зависимости от значения параметра Число перестановок), и в результате создаются эталонные распределения, которые можно сравнить с исходной глобальной и локальной L-статистикой Ли. Если исходное значение находится на крайних значениях (справа или слева) эталонного распределения, это означает, что исходное значение вряд ли является результатом случайного изменения и пространственная связь статистически значима. Значение p для глобальной L-статистики Ли возвращается в виде сообщения геообработки, а значения p и уровни значимости локальной L-статистики Ли возвращаются в виде полей выходного класса пространственных объектов. Дополнительные сведения см. в разделе ниже Выходные данные инструмента.

Примечание:

P-значения вычисляются путем подсчета количества перестановочных значений, которые являются более экстремальными, чем исходное значение, прибавления единицы и деления на количество перестановок плюс единица. Эта корректировка числителя и знаменателя сделана для небольших выборок и гарантирует, что p-значения никогда не будут равны нулю. Затем это значение удваивается, так что p-значение является результатом двусторонней проверки гипотезы. Сторона теста определяется по той стороне, которая имеет меньшую долю более экстремальных значений (измененные значения, которые больше или меньше исходного значения). P-значения локальной L-статистики Ли не корректируются для многократной проверки гипотез, поэтому учитывайте это при интерпретации любого конкретного локального p-значения.

Типы окрестностей

Глобальная и локальная L-статистика Ли требует наличия окрестности вокруг каждого объекта для оценки пространственной связи. Вы можете указать соседство каждого объекта с помощью параметра Тип соседства. Этот параметр содержит описанные ниже опции для определения объектов, которые используются в качестве соседей каждого объекта. Для всех типов окрестностей объект включается в свою собственную окрестность.

• Диапазон фиксированных расстояний — все объекты в пределах заданного расстояния (максимум 1000 объектов) используются в качестве соседей. Расстояние по умолчанию – это кратчайший расстояние, которое гарантирует каждому объекту как минимум 1 дополнительно соседа. Укажите расстояние в параметре Диапазон расстояний. Для полигонов, определение соседей используется расстояние между центроидами.

  

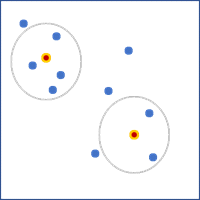
• K ближайших соседей — в качестве соседей используется фиксированное число ближайших объектов. Задайте значение в параметре Число соседей. Это значение не включает сам объект, поэтому количество объектов, используемых в расчетах, будет на единицу больше заданного значения. Для полигонов, определение соседей используется расстояние между центроидами.

  

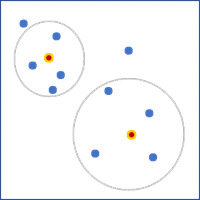
• Только совпадающие ребра — любые полигоны, имеющие общую границу с объектом, используются в качестве соседей. Этот опция применима только для полигональных объектов.

  

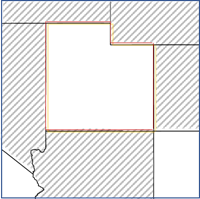
• Совпадающие ребра и углы — любые полигоны, имеющие общее ребро или угол с объектом, используются в качестве соседей. Этот опция применима только для полигональных объектов.

  

• Триангуляция Делоне - соседи будут определены путем совместного использования ребер или углов в их триангуляции Делоне (полигонах Тиссена), привязанных к выпуклой оболочке точек. Этот опция применима только для точечных объектов.

  

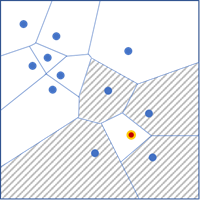
• Получить пространственные веса из файла — соседи и веса каждого объекта определяются файлом матрицы пространственных весов, указанным в параметре Файл матрицы весов. Создать файл можно с помощью инструментов Построить матрицу пространственных весов или Построить матрицу пространственных весов для сети.

Для диапазона расстояний и количества окрестностей соседей, расположенным ближе к объекту, можно присвоить более высокие веса, используя функцию ядра, которая уменьшается с увеличением расстояния. Чтобы применить большие веса к ближайшим соседям, выберите опцию Биквадратная для параметра Локальная схема весов.

Биквадратное ядро определяет веса по следующей формуле:

Функция ядра зависят от ширины полосы, которая влияет на то, как быстро веса уменьшаются с расстоянием. Ширина полосы для каждого ядра задается в параметре Ширина ядра. Для окрестности k ближайших соседей, если вы не укажете значение ширины канала, каждый объект будет использовать другую (адаптивную) ширину, равную расстоянию до (k+1)-го соседа объекта. Для окрестности диапазона расстояний ширина ядра по умолчанию равна тому же значению, что и параметр Диапазон расстояний.

Примечание:

Все объекты будут иметь вес, равный единице веса самого объекта, даже если в файле пространственных весов эти веса отсутствуют. Кроме того, веса для каждой окрестности объекта будут нормализованы и в сумме равны 1 (это называется стандартизацией строк).

Выходные данные инструмента

Инструмент возвращает множество выходных данных, которые вы можете использовать для исследования пространственной связи между двумя переменными анализа. Результаты возвращаются в виде сообщений геообработки, выходного класса пространственных объектов и точечной диаграммы.

Сообщения геообработки

Сообщения геообработки, возвращаемые инструментом, содержат значения, относящиеся к общей пространственной связи между двумя переменными анализа. В сообщениях отображаются следующие значения:

• Глобальное L Ли - коэффициент L-статистики Ли между двумя анализируемыми переменными. Значение будет в диапазоне от -1 до1. Положительные значения указывают на положительную пространственную связь, а отрицательные - на отрицательную пространственную связь. Значения, близкие к 0, указывают на то, что переменные пространственно не связаны. Статистика представляет собой комбинацию корреляции средних значений по окрестностям между переменными анализа и степенью пространственной автокорреляции каждой переменной анализа.
• Глобальное P-значение — p-значение двустороннего теста для определения статистически значимой пространственной связи. Небольшие значения p указывают на то, что глобальная L-статистика Ли является статистически значимой и не обусловлена случайными колебаниями. Если значение p является статистически значимым (менее 0,1 для 90-процентной значимости, менее 0,05 для 95-процентной значимости и менее 0,01 для 99-процентной значимости), а глобальная L-статистика Ли положительна, то две переменные анализа имеют значительную положительную связь в пространстве. Если значение p является статистически значительным, а глобальная L-статистика Ли отрицательна, то переменные анализа имеют значительную отрицательную связь в пространстве.
• Скаляр пространственного сглаживания (поле анализа 1) - значение от 0 до 1, указывающее степень пространственной автокорреляции первой переменной анализа. Значения, близкие к 1, указывают на сильную положительную пространственную автокорреляцию (высокие и низкие значения, как правило, группируются вместе), а значения, близкие к 0, указывают на сильную отрицательную пространственную автокорреляцию (высокие значения, как правило, окружены низкими значениями, и наоборот).
• Скаляр пространственного сглаживания (поле анализа 2) - значение от 0 до 1, указывающее степень пространственной автокорреляции второй переменной анализа.
• Корреляция Пирсона (исходная) - корреляция Пирсона между переменными анализа. Это значение полезно для сравнения с глобальной L-статистикой Ли, чтобы увидеть разницу между исходной корреляцией переменных и их пространственной связью.
• Корреляция Пирсона (средневзвешенные значения окрестности) - корреляция Пирсона между средневзвешенными значениями окрестности двух переменных анализа. Глобальная L-статистика Ли также приблизительно равна этому значению, умноженному на квадратные корни из скаляров пространственного сглаживания.

Глобальная L-статистика Ли, глобальное значение p и корреляция Пирсона (исходная) также возвращаются в качестве производных результатов этого инструмента.

Класс объектов и поля

Выходной класс пространственных объектов будет содержать следующие поля, обобщающие результаты локальной L-статистики Ли:

• Копии двух переменных анализа и поле ID источника для каждого входного объекта.
• Локальная пространственная связь (LOCAL_L) - локальная L-статистика Ли для каждого объекта. Значения выше 0 указывают на положительную пространственную связь между переменными анализа в данном местоположении, а значения ниже 0 - на отрицательную связь.
• Средневзвешенное значение окрестности (первая переменная анализа) (NWA_VAR1) - средневзвешенное значение окрестности первой переменной анализа для каждого объекта. Это значение представляет собой средневзвешенное значений объекта и его соседей с использованием весов, заданных параметрами Тип окрестности, Схема присвоения локальных весов и Ширина полосы ядра.
• Средневзвешенное значение окрестности (вторая переменная анализа) (NWA_VAR2) - средневзвешенное значение окрестности второй переменной анализа для каждого объекта.
• P-значение (P_VALUE) — значение p для двусторонней проверки гипотезы о статистической значимости локальной L-статистики Ли для каждого признака.
• Уровень значимости (SIG_LEVEL) — наивысший достигнутый уровень значимости локальной L-статистики Ли для каждого объекта. Возможные значения - Незначимый, Значимый на 90%, Значимый на 95% и Значимый на 99%.
• Категория локальной пространственной связи (ASSOC_CAT) — категория локальной пространственной связи для каждого объекта. Возможные значения: Not Significant, High-High, High-Low, Low-High и Low-Low. Например, Low-High означает, что объект является значимым по меньшей мере на 90 процентов, средневзвешенное значение окрестности для первой переменной анализа меньше среднего значения первой переменной анализа, а средневзвешенное значение окрестности второй переменной анализа больше среднего значения второй переменной анализа.
• Количество соседей (NUM_NBRS) — количество соседей (включая сам объект), которые использовались для расчета глобальной и локальной L-статистики Ли для каждого объекта.

Точечная диаграмма L-статистики Ли

Выходной векторный слой содержит точечную диаграмму L-статистики Ли, которая отображает средневзвешенные значения окрестности для первой переменной анализа на оси x и средневзвешенные значения окрестности второй переменной анализа на оси y, а также линию тренда, соответствующую данным. Пунктирные горизонтальные и вертикальные линии также проводятся по среднему значению каждой анализируемой переменной. Эти линии делят точечную диаграмму на четыре квадранта и используются для распределения точек по категориям локальной пространственной связи. Например, статистически значимыми объектами в верхнем левом квадранте будет категория Low-High (светло-синие).

Диаграмма также может быть использована для определения отдельных объектов, которые отклоняются от общих тенденций остальных объектов. Например, вы можете выбрать отдельные точки на точечной диаграмме, которые находятся далеко от линии тренда, для дальнейшего изучения этих объектов. Вы можете обнаружить, что эти объекты группируются на карте и показывают региональные закономерности для пространственных связей, которые в противном случае было бы трудно обнаружить.

Лучшие практики и ограничения

При использовании этого инструмента необходимо учитывать следующее:

• Выбросы (значения, которые намного больше или меньше остальных значений) в любой из переменных анализа сильно влияют на результаты. Рекомендуется создать гистограммы для каждой анализируемой переменной, чтобы определить, присутствуют ли выбросы, и удалить любые объекты, содержащие выбросы в любой из переменных. Вы также можете использовать Data Engineering для выявления выбросов.
• При использовании этого инструмента предполагается, что существует линейная зависимость между средневзвешенными значениями окрестности двух переменных анализа. Если значения на точечной диаграмме L-статистики Ли отображают нелинейную структуру, вы можете использовать инструмент Трансформировать поле, чтобы применить преобразования к переменным анализа для линеаризации отношения и повторно запустить инструмент с преобразованными значениями.
• Статистически значимое значение p (обычно менее 0,05) не обязательно означает, что между этими двумя переменными существует взаимная корреляция. Однако это может означать только то, что одна или обе переменные имеют высокую пространственную автокорреляцию. Чтобы интерпретировать статистически значимое p-значение, проанализируйте значения глобальной L-статистики Ли, корреляцию между средними значениями по окрестностям и скаляр пространственного сглаживания для каждой переменной. В совокупности эти значения позволяют интерпретировать источник статистической значимости: автокорреляцию, перекрестную корреляцию или и то, и другое вместе. Если значение p является статистически значимым, а глобальная L-статистика Ли и корреляция между средними значениями по окрестностям очень близки к 0 и скаляры пространственного сглаживания близки к 1, это, вероятно, означает, что каждая из переменных сильно автокоррелирована, но взаимная корреляция между ними незначительна.
• Рекомендуется использовать не менее 50 входных объектов и включить не менее 8 соседей для каждого объекта.

Формулы

Этот раздел содержит формулы для всей статистики, рассчитанной с помощью инструмента. См. статьи в разделе Ссылки ниже для получения информации о производных и дополнительной информации.

Во всех формулах x относится к первой переменной анализа, а y - ко второй. Тильда (~) над переменной показывает, что это средневзвешенное значение окрестности. Веса для каждой окрестности нормализованы, чтобы в сумме они были равны 1. Черта над переменной показывает, что это невзвешенное среднее по всем n входным объектам. Нижний индекс i означает один входной объект. Все суммы в формулах суммируются по всем входным объектам.

Глобальная L-статистика Ли рассчитывается по следующей формуле:

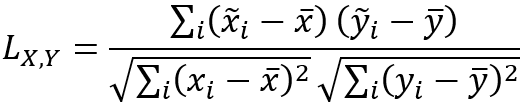
Глобальная L-статистика Ли также приблизительно равна произведению квадратных корней из скаляров пространственного сглаживания и корреляции между средневзвешенными значениями окрестностей следующим образом:

Скаляры пространственного сглаживания вычисляются по следующим формулам:

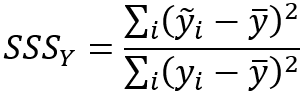
Корреляция между средневзвешенными значениями окрестностей рассчитывается по следующей формуле:

Локальная L-статистика Ли рассчитывается по следующей формуле:

Глобальная L-статистика Ли равна среднему значению локальной L-статистики Ли следующим образом:

Справочная информация

Для внедрения этого инструмента были использованы следующие ресурсы:

• Lee, Sang-Il. «Разработка двумерной пространственной меры ассоциации: интеграция r Пирсона и I Морана». Journal of geographical systems 3 (2001): 369-385. https://doi.org/10.1007/s101090100064.
• Lee, Sang-Il. "Обобщенный рандомизационный подход к локальным измерениям пространственной ассоциации". Geographical Analysis 41.2 (2009): 221-248. https://doi.org/10.1111/j.1538-4632.2009.00749.x.