[ディメンションの削減 (Dimension Reduction)] ツールは、主成分分析 (PCA) またはランク縮小線形判別分析 (LDA) を使用して、可能な限り高い分散量をより少ない成分に集約することにより、連続変数のセットの次元数を減らします。変数は入力テーブルまたはフィーチャ レイヤーのフィールドとして指定され、新しい変数を表す新しいフィールドは、出力テーブルまたはフィーチャクラスに保存されます。新しいフィールドの数は、元の変数の数よりも少なくなりますが、元のすべての変数から可能な限り高い分散量が維持されます。
変数間の多変量関係を調べ、必要なメモリと処理時間がデータの次元数に依存する機械学習アルゴリズムの計算コストを削減するために、次元削減は広く使用されます。分析または機械学習アルゴリズムで元のデータの代わりに成分を使用すると、多くの場合、より少ない計算リソースを消費しながら、同等の (またはよりよい) 結果を得られます。
成分を使用して連続変数の値を予測する分析または機械学習の方法を実行する場合は、PCA を使用することをお勧めします。LDA ではさらに、各レコードを、土地利用カテゴリなどのカテゴリに分類する必要があります。数値分析フィールドに基づいてカテゴリ変数のカテゴリを分類するために成分が使用される分析または機械学習の方法を実行するには、PCA を使用することをお勧めします。
適用例
このツールは次のようなシナリオで使用できます。
- 同時に視覚化することが難しい多くのフィールドを持つフィーチャクラスがあります。データセットを 2 次元に減らすことで、チャートを使用してデータを視覚化し、2 次元のフィールド間の多変量相互作用を確認することができます。
- [空間関係のモデリング] ツールセットの解析ツール、たとえば [一般化線形回帰 (Generalized Linear Regression)] ツールや [地理空間加重回帰分析 (Geographically Weighted Regression) (GWR)] ツールを使用することをお勧めします。ただし、フィールドの多くは相互に高度な相関関係があります。説明変数の次元数を減らすことにより、解析ツールはより安定し、トレーニング データに過剰適合しにくくなります。
- 入力変数の数に応じて実行時間が急速に増加する機械学習メソッドを実行しています。次元数を減らすことで、メモリ使用量と処理時間を削減しながら同等の解析結果を得ることができます。
PCA の仕組み
PCA は、すべての分析フィールドの全分散の特定の割合をそれぞれが捉える成分を順次構築することによって分析を行います。各成分自体は、各分析フィールドの線形結合 (加重和) であり、加重は成分負荷と呼ばれます。分析フィールドとともに、荷重は固有ベクトルを形成し、成分への各分析フィールドの寄与を示します。成分は、成分によって維持される分散の合計を表す固有値にも関連付けられています。
次の図に示すように、2 つの分析フィールドの場合、PCA をデータ空間内の回転軸として幾何学的に視覚化できます。この回転により、新しい軸の変動率が最大になります。
左の画像では、各ポイントは、X 軸と Y 軸に 2 つの分析フィールドの値が 2 次元でプロットされた入力テーブルのレコードです。青い軸の長さは、2 つの変数のそれぞれの分散を表しています。2 つの青い矢印の長さはほぼ等しく、2 つの変数の分散がほぼ等しいことを示しています。中央の画像では、変数間の線形関係をより適切に表すために軸が回転しています。緑の軸の 1 本は他の軸よりわずかに長く、その方向の分散がより大きいことを示しています。ただし、この回転は最適ではありません。右の画像は、変数間の線形関係と一致する PCA によって検出された最適な回転を示しています。この回転により、分散が最も大きい赤い軸が生成されます。大きい方の赤い軸は第 1 主成分に対応し、2 次元データを 1 次元で最もよく表しています。3 つのすべての画像で、元の変数の合計分散量は同じですが、右側の画像では、第 1 成分に可能な限り最大の分散量が割り当てられており、第 2 成分には可能な限り最小の分散量が残っています。
各成分の固有値および固有ベクトルは、[固有ベクトル出力テーブル] および [固有ベクトル出力テーブル] パラメーターを使用して確認できます。固有ベクトルテーブルには、各成分の負荷を表示したバー チャートが含まれます。PCA の数学的な詳細説明については、「参考資料」をご参照ください。
ランク縮小線形判別分析の詳細
LDA (RR-LDA または Reduced-Rank LDA と略されることもあります) は、カテゴリ変数のクラス間の分離可能性を最大化する成分を順次構築することによって分析を行います。この方法は、カテゴリ変数のカテゴリ分類時に最高の正解率を維持しながら、連続分析フィールドの次元を削減することを目的とします。PCA と同様に、LDA の成分も固有ベクトルと固有値に関連付けられ、各成分への分析フィールドの寄与と、各成分によって維持される分散量を表します。
2 つの連続分析変数と 2 つのカテゴリを持つカテゴリ変数の場合、LDA には回転を含む 2D 幾何学的解釈もあります。下の画像は、各ポイントが入力データセットのレコードを表すデータセットを示しています。X 軸と Y 軸は 2 つの連続分析フィールドで、ポイントはカテゴリに基づいて赤または青に色分けされています。赤と青の分布は、Y 軸に投影されたときのカテゴリの分布です。クラスの分布にはある程度の分離可能性はありますが、重複が大きく、分離は困難です。X 軸への投影で、同様に分離の不足が発生します。
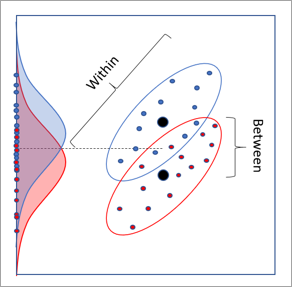
下の画像は、LDA によって決定された最適な軸回転を示しています。この回転により、カテゴリの分布間の分離が最大になり、カテゴリの分類率が最も高くなります。
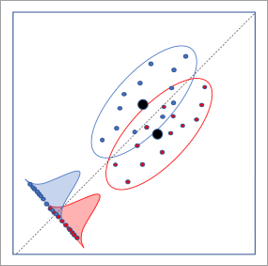
2 つ以上の成分が作成された場合、出力フィーチャには [線形判別] 散布図が含まれます。最初および 2 番目の成分の値が軸上にプロットされ、ポイントはそのカテゴリによって色付けされます。最初の 2 つの成分がカテゴリの区別に十分な情報を保持している場合、散布図内のポイントはカテゴリ別にクラスター化されることがあります。
各成分の固有値および固有ベクトルは、[固有ベクトル出力テーブル] および [固有ベクトル出力テーブル] パラメーターを使用して表示できます。固有ベクトルテーブルには、各成分の負荷を表示したバー チャートが含まれます。LDA の数学的な詳細説明については、「参考資料」をご参照ください。
コンポーネント数の決定
次元削減で最も重要な選択の 1 つは、作成する成分の数です。これは、削減する入力データの次元数の選択に相当します。たとえば、最大 4 つの変数でのみ効率的に機能する機械学習法など、目的の分析に基づいて必要な成分の数がわかっている場合があります。また、元のデータの分散全体の 90% を維持するために必要な主成分数を使用する場合もあります。成分の数を最小化することと維持される分散の割合を最大化することの間で、バランスをとる必要がある場合もあります。
どちらのデータ次元削減法も、p 分析フィールドでは、ith 成分によって説明される分散率は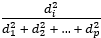 
です。ここで、di は ith 成分の固有値です。各順次成分は、1 つ前の成分よりも、全分散に対し低いパーセンテージを維持します。
ツールで使用される成分の数は、[成分の最小数] および [維持する分散の最小パーセント] パラメーターに値が指定されているかどうかによって異なります。
- 一方のパラメーターが指定され、他方が指定されない場合、指定されたパラメーターが成分の数を決定します。成分の数は、指定された最小値を満たすために必要な最小数と同じです。
- パラメーターが両方とも指定された場合は、結果として得られる 2 つの成分数のうち大きい方が使用されます。
- どちらのパラメーターも指定されない場合、成分数はいくつかの統計方法を使用して決定されます。ツールは、各方法で推奨される最大数の成分を使用します。どちらの次元削減方法にも、ブロークン スティック法とバートレットの球面性検定が含まれます。PCA では、[順列の数] パラメーターの値がゼロより大きい場合、順列テストも行われます。統計テストの結果は、ジオプロセシング メッセージとして表示されます。3 つのテストの数学的な詳細説明については、「参考資料」セクションをご参照ください。
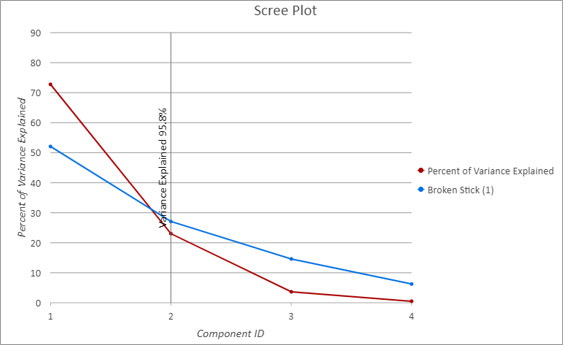
出力固有値テーブルには、各成分によって維持される分散率を示す、「スクリー プロット」と呼ばれるカスタマイズされたライン チャートが含まれています。以下のスクリー プロットでは、X 軸は各連続成分を示し、赤い線は各成分によって説明される分散率を示しています。赤い線が減少し、新しい各成分が前の成分よりも分散量が小さいことを示しています。X 軸の成分 2 の上にある黒い縦線は、ツールが 2 つの成分を使用し、元の変数の合計分散の 95.8 パーセントを維持していることを示しています。青い線は、成分の最適な数を推定するために使用されたブロークン スティック法の結果を示しています。成分の最適数は、多くの場合、赤と青の線が交差する場所に対応しており、成分数が一致していることを示しています。
ベスト プラクティスおよび制限
このツールを使用する場合、以下を考慮してください。
- PCA の場合、この分析の結果は、変数がスケーリングされているかどうかによって異なります。PCA は全分散を成分に分割するので、分析フィールドの生の値が大きいほど、全分散に対するより高い割合がそれに関連付けられます。分散が 1 に等しくなるよう各分析フィールドをスケーリングすると、この影響がなくなります。たとえば、分析フィールドがスケーリングされている場合、フィートで測定されたデータとメートルで測定されたデータは同じ成分になります。スケーリングされていない場合、フィートで測定されたデータは、メートルで測定された同じデータよりも第 1 成分に大きく影響します。これは、フィートで測定された距離値が、メートルで測定された同じ距離値 (1 メートル = 3.2808 フィート) よりも大きいためです。
- PCA は、すべての分析フィールド間の線形関係を想定して、固有値と固有ベクトルを推定します。分析フィールド間の関係が非線形である場合、PCA はこれらの関係を正確に捉えません。分析変数の散布図マトリックスを作成し、非線形パターンを探すことをお勧めします。非線形パターンが見つからない場合は、[フィールドの変換 (Transform Field)] ツールを使用して関係を線形化することができます。
参考資料
PCA とランク低下 LDA の詳細については、次の参考資料をご参照ください。
- James, G., Witten, D., Hastie, T., Tibshirani, R. (2014). "An Introduction to Statistical Learning: with Applications in R." Springer Publishing Company, Incorporated. https://doi.org/10.1007/978-1-4614-7138-7
成分の数を決定する方法の詳細については、次の参考資料をご参照ください。
- Peres-Neto, P., Jackson, D., Somers, K. (2005). "How many principal components? Stopping rules for determining the number of non-trivial axes revisited." Computational Statistics & Data Analysis. 49.4: 974-997. https://doi.org/10.1016/j.csda.2004.06.015.